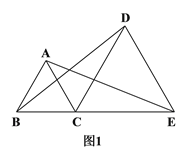
题目内容
【题目】如图,抛物线y= ![]() x2+
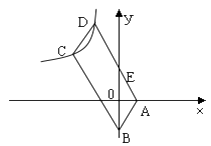
x2+ ![]() x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,
x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6, ![]() )在抛物线上,直线AC与y轴交于点D.
)在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m,求AN的长(用含m的代数式表示).
【答案】
(1) 解:把C点坐标代入抛物线解析式可得 ![]() , 解得c=﹣3,∴抛物线解析式为
, 解得c=﹣3,∴抛物线解析式为 ![]() , 令y=0可得
, 令y=0可得 ![]() ,解得x=﹣4或x=3,∴A(﹣4,0),设直线AC的函数表达式 为y=kx+b(k≠0),把A、C坐标代入可得:
,解得x=﹣4或x=3,∴A(﹣4,0),设直线AC的函数表达式 为y=kx+b(k≠0),把A、C坐标代入可得: 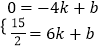 ,解得:
,解得: 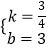 ,∴直线AC的函数表达式为
,∴直线AC的函数表达式为 ![]()
(2) 解:①∵在Rt△AOB中,tan∠OAB= ![]() =
= ![]() ,在RtAOD中,tan ∠OAD=
,在RtAOD中,tan ∠OAD= ![]() =
= ![]() ,∴∠OAB=∠OAD,∵在Rt△POQ中,M为PQ的中点,∴OM=MP,∴∠MOP=∠MPO,且∠MOP=∠AON,∴∠APM=∠AON,∴△APM∽△AON;
,∴∠OAB=∠OAD,∵在Rt△POQ中,M为PQ的中点,∴OM=MP,∴∠MOP=∠MPO,且∠MOP=∠AON,∴∠APM=∠AON,∴△APM∽△AON;
②如图,过点M作ME⊥x轴于点E,

则OE=EP,∵点M的横坐标为m,∴AE=m+4,AP=2m+4,∵tan∠OAD= ![]() ,∴co s∠EAM=cos∠OAD=
,∴co s∠EAM=cos∠OAD= ![]() ,∴
,∴ ![]() =
= ![]() ,∴AM=
,∴AM= ![]() AE=
AE= ![]() , ∵△APM∽△AON,∴
, ∵△APM∽△AON,∴ ![]() , 即
, 即 ![]() ,∴AN=
,∴AN= ![]()
【解析】(1)把C点坐标代入抛物线解析式,求出抛物线解析式,得到点A的坐标,把A、C坐标代入,求出直线AC的函数表达式;(2)根据解直角三角形,得到∠OAB=∠OAD,再由已知条件得到△APM∽△AON;得出比例,求出AN的值.
【考点精析】通过灵活运用相似三角形的判定与性质和解直角三角形,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.