题目内容
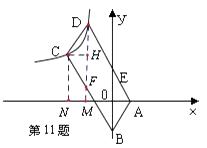
【题目】如图，四边形ABCD是平行四边形，顶点A、B的坐标分别是A（1，0），B（0，﹣2），顶点C、D在双曲线 
上，边AD与y轴相交于点E， 
=10，则k的值是（ ）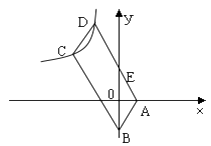
A.-16
B.-9
C.-8
D.-12
【答案】D
【解析】过点D作DM⊥x轴，垂足为F，交BC与点F，过点C分别作CN⊥x轴、CH⊥DM，垂足分别为N、H，
∵S四边形BEDC=S△ABE=10，
∴S△ABE=2，即 
×BE·AO=2，
∵A（1，0），
∴OA=1，
∴BE=4，
∵四边形ABCD是平行四边形，
∴CD=AB，∠ABC=∠CDA，
∵DM//BE，
∴∠EBC=∠EDM，
∴∠CDH=∠ABO，
∵∠AOB=∠CDH，
∴△CDH≌△ABO，
∴CH=AO=1，DH=BO=2，
又∵BC//AD，
∴四边形BEDF是平行四边形，
∴DF=BE=4，
∴S△CDF= ×4×1=2，
∴S四边形BEDF=10-2=8，即BE·OM=8，
∴OM=2，
∴M（-2，0），
∴设D（-2，m），C（-3，m-2），
∴-2m=-3（m-2）=k，∴m=6，∴k=-12；
所以答案是：D．
【考点精析】掌握平行线的判定与性质和三角形的面积是解答本题的根本，需要知道由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；三角形的面积=1/2×底×高．
【题目】某班同学响应“阳光体育运动”号召，利用课外活动积极参加体育锻炼，每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练，训练前后都进行了测试，现将项目选择情况及训练后篮球定时定点投篮进球数（每人投10次）进行整理，作出如下统计图表．
进球数（个） | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
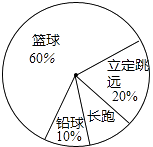
请你根据图表中的信息回答下列问题：
（1）训练后篮球定时定点投篮人均进球数为个；进球数的中位数为个，众数为个；
（2）该班共有多少学生；
（3）根据测试资料，参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%，求参加训练之前的人均进球数（保留一位小数）．
