题目内容
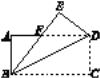
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE与AD相交于点F,∠EDF=38°,则∠DBE的度数是( )
A. 25° B. 26° C. 27° D. 38°
【答案】B
【解析】
由折叠的性质易得∠E=∠C=90°,∠EBD=∠CBD,由AD∥BC可得∠FDB=∠CBD,由此可得∠EBD=∠FDB,由∠EDF=38°可得∠EFD=52°,这样结合∠EFD=∠EBD+∠FBD,即可得到∠DBE=26°.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°,
∴∠FDB=∠CBD,
∵△EBD是由△CBD沿着BD折叠形成的,
∴∠E=∠C=90°,∠EBD=∠CBD,
∴∠EFD=180°-90°-∠EDF=90°-38°=52°,∠EBD=∠FDB,
又∵∠EFD=∠EBD+∠FDB,
∴∠EBD=![]() ∠EFD=26°.
∠EFD=26°.
故选B.

练习册系列答案
相关题目