题目内容
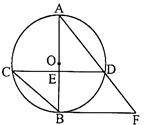
如图,以BC为直径的圆0交∆CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2 =AF.AC.
小题1:求△ANM?△ENM;
小题2:求证:FB是圆O的切线
小题3:证明四边形AMEN是菱形.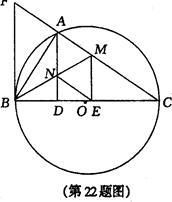
小题1:求△ANM?△ENM;
小题2:求证:FB是圆O的切线
小题3:证明四边形AMEN是菱形.

小题1:证明:因为BC是圆0的直径,
所以:∠BAC=900 (1分)
又EM⊥BC,BM平分∠ABC,
所以:AM="ME." ∠AMN=∠EMN
又MN=MN
所以:∆ANM?∆ENM
小题2:因为:AB2=AF?AC,

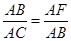
又∠ABF=∠C
所以:∆ABF~∆ACB (4分)
所以:∠ABF=∠C
又∠FBC="∠ABC+∠FBA=" 900,
.’.FB是圆O的切线
小题3:解:由(1)得AN="EN,AM=EM," ∠AMN=∠EMN
又:AN//ME
所以:∠ANM=∠EMN (7分)
所以:∠AMN=∠ANM (8分)
所以:AN=AM
AM=ME+EN=AN
所以:四边形AMEN是菱形 (10分)
(1)利用角平分线的性质定理,可以得出AM=ME,∠AMN=∠EMN,再利用SAS可证出:△ANM≌△ENM
(2)利用相似三角形的判定可证出△ABF∽△ACB,从而得出∠ABF=∠C,那么可以得到∠CBF=90°
(3)利用(1)中的结论先证出∠AMN=∠ANM,可以得到AM=ME=EN=AN,从而得出四边形AMEN是菱形,再求出△BND∽△BME,利用比例线段可求出ME的长,再利用菱形的面积公式可计算出菱形的面积.
(2)利用相似三角形的判定可证出△ABF∽△ACB,从而得出∠ABF=∠C,那么可以得到∠CBF=90°
(3)利用(1)中的结论先证出∠AMN=∠ANM,可以得到AM=ME=EN=AN,从而得出四边形AMEN是菱形,再求出△BND∽△BME,利用比例线段可求出ME的长,再利用菱形的面积公式可计算出菱形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
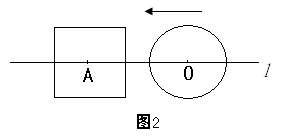
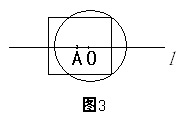
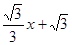 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左平平移,当⊙P向左平移 个单位长度时,⊙P与该直线相切.
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左平平移,当⊙P向左平移 个单位长度时,⊙P与该直线相切. 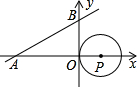
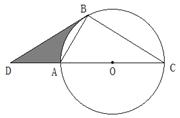
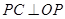 ,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .
,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .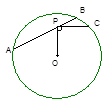
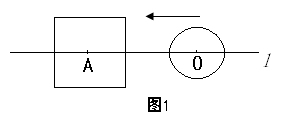
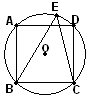
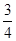 ,求线段AD、CD的长.
,求线段AD、CD的长.