题目内容
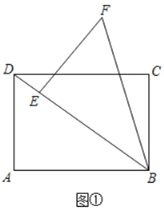
【题目】(操作)BD是矩形ABCD的对角线,AB=4,BC=3.将△BAD绕着点B顺时针旋转α度(0°<α<360°)得到△BEF,点A、D的对应点分别为E、F.若点E落在BD上,如图①,则DE=______.
(探究)当点E落在线段DF上时,CD与BE交于点G.其它条件不变,如图②.
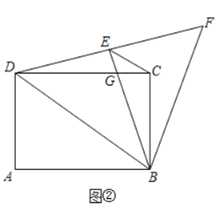
(1)求证:△ADB≌△EDB;
(2)CG的长为______.
(拓展)连结CF,在△BAD的旋转过程中,设△CEF的面积为S,直接写出S的取值范围.
【答案】[操作]1;[探究](1)见解析;(2)![]() ;[拓展] S的取值范围为
;[拓展] S的取值范围为![]() .
.
【解析】
[操作】由勾股定理得出BD=![]() =5,由旋转的性质得出BE=BA=4,即可得出答案;
=5,由旋转的性质得出BE=BA=4,即可得出答案;
[探究](1)由HL证明Rt△ADB≌Rt△EDB即可;
(2)由矩形的性质和折叠的性质得出∠CDB=∠EBD,证出DG=BG,设CG=x,则DG=BG=4﹣x,在Rt△BCG中,由勾股定理得出方程,解方程即可;
[拓展]由题意得出点C到EF的距离最小时,△CEF的面积最小;点C到EF的距离最大时,△CEF的面积最大;当点E在BC的延长线上时,点C到EF的距离最小,此时CE⊥EF,CE=BE﹣BC=1,由三角形面积公式得出△CEF的面积S最小=![]() EF×CE=
EF×CE=![]() ;当点E在CB的延长线上时,点C到EF的距离最大,此时CE⊥EF,CE=BE+BC=7,由三角形面积公式得出△CEF的面积S最大=
;当点E在CB的延长线上时,点C到EF的距离最大,此时CE⊥EF,CE=BE+BC=7,由三角形面积公式得出△CEF的面积S最大=![]() EF×CE=
EF×CE=![]() ;即可得出答案.
;即可得出答案.
[操作]
解:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=3,
∴![]() ,
,
由旋转的性质得:BE=BA=4,
∴DE=BD-BE=5-4=1;
故答案为:1;
[探究](1)证明:由旋转的性质得:△BEF≌△BAD,
∴∠BEF=∠A=90°,BE=BA,
∴∠BED=180°-∠BEF=90°=∠A,
在Rt△ADB和Rt△EDB中,![]() ,
,
∴Rt△ADB≌Rt△EDB(HL);
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,CD=AB=4,∠BCD=90°,
∴∠ABD=∠CDB,
由折叠的性质得:∠ABD=∠EBD,
∴∠CDB=∠EBD,
∴DG=BG,
设CG=x,则DG=BG=4-x,
在Rt△BCG中,由勾股定理得:x2+32=(4-x)2,
解得:![]() ,即
,即![]() ;
;
故答案为:![]() ;
;
[拓展] 解:∵△CEF的边长EF=AD=3,
∴点C到EF的距离最小时,△CEF的面积最小;点C到EF的距离最大时,△CEF的面积最大;
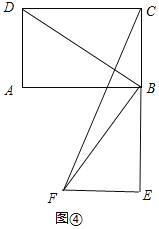
当点E在BC的延长线上时,点C到EF的距离最小,如图③所示:
此时CE⊥EF,CE=BE-BC=4-3=1,
△CEF的面积![]() ;
;
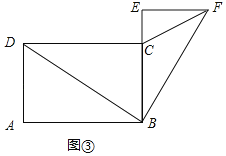
当点E在CB的延长线上时,点C到EF的距离最大,如图④所示:
此时CE⊥EF,CE=BE+BC=4+3=7,
△CEF的面积![]() ;
;
∴S的取值范围为![]() .
.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案