题目内容
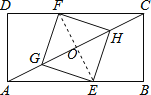
【题目】如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是 .

【答案】5
【解析】
试题分析:首先连接EF交AC于O,由矩形ABCD中,四边形EGFH是菱形,易证得△CFO≌△AOE(AAS),即可得OA=OC,然后由勾股定理求得AC的长,继而求得OA的长,又由△AOE∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
解:连接EF交AC于O,
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,
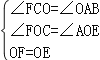 ,
,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC=![]() =4
=4![]() ,
,
∴AO=![]() AC=2
AC=2![]() ,
,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AE=5.
故答案为5.

 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?





