题目内容
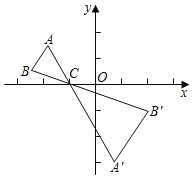
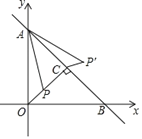
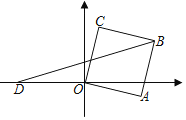
【题目】如图,正方形ABCO的边长为![]() ,OA与x轴正半轴的夹角为15°,点B在第一象限,点D在x轴的负半轴上,且满足∠BDO=15°,直线y=kx+b经过B、D两点,则b﹣k=_____.
,OA与x轴正半轴的夹角为15°,点B在第一象限,点D在x轴的负半轴上,且满足∠BDO=15°,直线y=kx+b经过B、D两点,则b﹣k=_____.
【答案】2﹣![]() .
.
【解析】
连接OB,过点B作BE⊥x轴于点E,根据正方形的性质可得出∠AOB的度数及OB的长,结合三角形外角的性质可得出∠BDO=∠DBO,利用等角对等边可得出OD=OB,进而可得出点D的坐标,在Rt△BOE中,通过解直角三角形可得出点B的坐标,由点B,D的坐标,利用待定系数法可求出k,b的值,再将其代入(b﹣k)中即可求出结论.
解:连接OB,过点B作BE⊥x轴于点E,如图所示.
∵正方形ABCO的边长为![]() ,
,
∴∠AOB=45°,OB=![]() OA=2.
OA=2.
∵OA与x轴正半轴的夹角为15°,
∴∠BOE=45°﹣15°=30°.
又∵∠BDO=15°,
∴∠DBO=∠BOE﹣∠BDO=15°,
∴∠BDO=∠DBO,
∴OD=OB=2,
∴点D的坐标为(﹣2,0).
在Rt△BOE中,OB=2,∠BOE=30°,
∴BE=![]() OB=1,OE=
OB=1,OE=![]() =
=![]() ,
,
∴点B的坐标为(![]() ,1).
,1).
将B(![]() ,1),D(﹣2,0)代入y=kx+b,
,1),D(﹣2,0)代入y=kx+b,
得: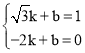 ,
,
解得: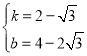 ,
,
∴b﹣k=4﹣2![]() ﹣(2﹣
﹣(2﹣![]() )=2﹣
)=2﹣![]() .
.
故答案为:2﹣![]() .
.


练习册系列答案
相关题目