题目内容
【题目】设A、B、C、D为平面上任意四点,如果其中任意三点不在同一直线上,则△ABC、△ABD、△ACD、△BCD中至少存在一个三角形的某个内角满足( )
A.不超过 15°B.不超过 30°C.不超过 45°D.以上都不对
【答案】C
【解析】
假设结论的反面成立,即三角形的三个内角都大于45°,从假设出发推出矛盾:四边形内角和大于360°矛盾.
解:△ABC、△ABD、△ACD、△BCD中至少存在一个三角形的某个内角满足不超过 45°,证明如下:
证明:假设A、B,C、D四点,任选三点构成的三角形的三个内角都大于45°,
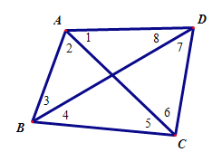
则∠1>45°,∠2>45°,∠3>45°,∠4>45°,∠5>45°,∠6>45°,∠7>45°,∠8>45°,
∴∠1+∠2+∠3+∠4+∠5+∠6°+∠7+∠8>360°,
即四边形ABCD的内角和大于360°,与四边形内角和等于360°矛盾;
故选:C.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):

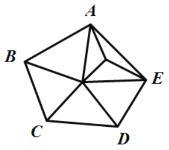
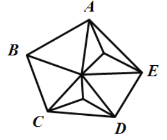
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.