题目内容
【题目】已知:∠AOB= ![]() °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解.
(1)若 ![]() =30,则∠AOC=________.
=30,则∠AOC=________.
(2)若 ![]() =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
(3)若0< ![]() <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用 ![]() 的代数式表示).
的代数式表示).
【答案】(1)120°或60°(2)示意图详见解析,20°;(3)![]() .
.
【解析】
(1)由OB⊥OC可得出∠BOC=90°,分射线OA、OC在射线OB同侧和两侧讨论,结合图形即可得出结论;
(2)分射线OA、OC在射线OB同侧和两侧讨论,根据角平分线定义即可得出∠COE和∠COF的大小,结合图形即可求出∠EOF的度数;
(3)分射线OA、OC在射线OB同侧和两侧讨论,根据角平分线定义即可得出∠COE和∠COF的大小,结合图形即可求出∠EOF的度数.
根据题意画出图形,如图所示.
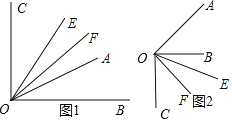
(1)∵OB⊥OC,
∴∠BOC=90°.
当射线OA、OC在射线OB同侧时,∠AOC=∠BOC-∠AOB=60°;
当射线OA、OC在射线OB两侧时,∠AOC=∠AOB+∠BOC=120°.
故答案为:60°或120°.
(2)当射线OA、OC在射线OB同侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC-∠AOB)=
(∠BOC-∠AOB)=![]() ×(90°-40°)=25°,∠COF=
×(90°-40°)=25°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COF-∠COE=45°-25°=20°;
当射线OA、OC在射线OB两侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOB)=
(∠BOC+∠AOB)=![]() ×(90°+40°)=65°,∠COF=
×(90°+40°)=65°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COE-∠COF=65°-45°=20°.
综上可知:∠EOF的度数为20°.
(3)当射线OA、OC在射线OB同侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC-∠AOB)=
(∠BOC-∠AOB)=![]() ×(90°-α°)=45°-
×(90°-α°)=45°-![]() °,∠COF=
°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COF-∠COE=45°-(45°-![]() °)=
°)=![]() °;
°;
当射线OA、OC在射线OB两侧时,
∵射线OE平分∠AOC,射线OF平分∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOB)=
(∠BOC+∠AOB)=![]() ×(90°+α°)=45°+
×(90°+α°)=45°+![]() °,∠COF=
°,∠COF=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠COE-∠COF=(45°+![]() °)-45°=
°)-45°=![]() .
.
故答案为:![]() .
.