题目内容
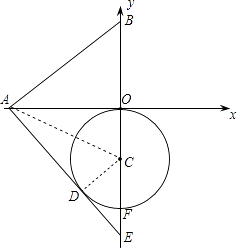
【题目】如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( ) 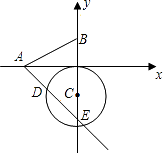
A.3
B.![]()
C.![]()
D.4
【答案】B
【解析】解:当射线AD与⊙C相切时,△ABE面积的最大.
连接AC,
∵∠AOC=∠ADC=90°,AC=AC,OC=CD,
∴Rt△AOC≌Rt△ADC,
∴AD=AO=2,
连接CD,设EF=x,
∴DE2=EFOE,
∵CF=1,
∴DE= ![]() ,
,
∴△CDE∽△AOE,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得x= ![]() ,
,
S△ABE= ![]() =
= ![]() =
= ![]() .
.
故选:B.
【考点精析】掌握三角形的面积和切线的性质定理是解答本题的根本,需要知道三角形的面积=1/2×底×高;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目