题目内容
【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .
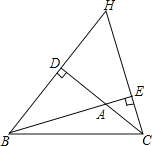
【答案】(1)①∠DBA=∠ECA,证明见解析;②80°;(2)50°或130°.
【解析】试题分析:(1)①根据同角的余角的相等即可说明∠DBA=∠ECA,根据四边形的内角和是360°,求得∠DHE的度数;
(2)分△ABC是锐角三角形,钝角三角形两种情况讨论求解即可.
(1)①∠DBA=∠ECA.
证明:∵BD、CE是△ABC的两条高,
∴∠BDA=∠AEC=90°,
∴∠DBA+∠BAD=∠ECA+∠EAC=90°,
又∵∠BAD=∠EAC,
∴∠DBA=∠ECA;
②∵BD、CE是△ABC的两条高
∴∠HDA=∠HEA=90°
在四边形ADHE中,∠DAE+∠HDA+∠DHE+∠HEA=360°
又∵∠HDA=∠HEA=90°,∠DAE=∠BAC=100°
∴∠DHE=360°-90°-90°-100°=80°
(2)①△ABC是锐角三角形时,∠DHE=180°-50°=130°;
②△ABC是钝角三角形时,∠DHE=∠A=50°;
故答案为:50°或130°.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目