题目内容
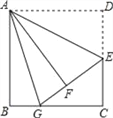
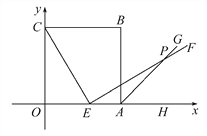
【题目】如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
(1)求证:CE=EP.
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在点M的坐标为(0,2).
【解析】(1)在OC上截取OK=OE.连接EK,求出∠KCE=∠CEA,根据ASA推出△CKE≌△EAP,根据全等三角形的性质得出即可;
(2)过点B作BM∥PE交y轴于点M,根据ASA推出△BCM≌△COE,根据全等三角形的性质得出BM=CE,求出BM=EP.根据平行四边形的判定得出四边形BMEP是平行四边形,即可求出答案.
(1)在OC上截取OK=OE.连接EK,如图1.
∵OC=OA,∠COA=∠BA0=90°,∠OEK=∠OKE=45°.
∵AP为正方形OCBA的外角平分线,∴∠BAP=45°,∴∠EKC=∠PAE=135°,∴CK=EA.
∵EC⊥EP,∴∠CEF=∠COE=90°,
∴∠CEO+∠KCE=90°,∠CEO+∠PEA=90°,∴∠KCE=∠CEA.
在△CKE和△EAP中,∵  ,
,
∴△CKE≌△EAP,∴EC=EP;
(2)y轴上存在点M,使得四边形BMEP是平行四边形.
如图,过点B作BM∥PE交y轴于点M,连接BP,EM,如图2,
则∠CQB=∠CEP=90°,所以∠OCE=∠CBQ.
在△BCM和△COE中,∵ ,
,
∴△BCM≌△COE,∴BM=CE.
∵CE=EP,∴BM=EP.
∵BM∥EP,∴四边形BMEP是平行四边形.
∵△BCM≌△COE,∴CM=OE=3,∴OM=CO﹣CM=2.
故点M的坐标为(0,2).


 金博士一点全通系列答案
金博士一点全通系列答案