题目内容
【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点.观察图象可知:当x=﹣3或1时,y1=y2 .
交于A(1,3)和B(﹣3,﹣1)两点.观察图象可知:当x=﹣3或1时,y1=y2 . 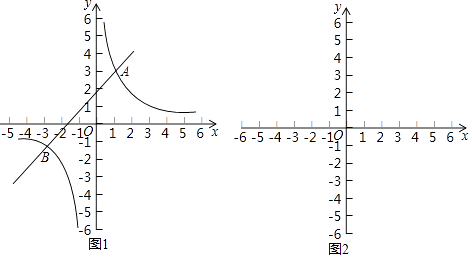
(1)通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集 .
的解集 .
(2)参考观察函数的图象方法,解决问题:关于x的不等式x2+a﹣ ![]() <0(a>0)只有一个整数解,则a的取值范围 .
<0(a>0)只有一个整数解,则a的取值范围 .
【答案】
(1)x>1或﹣3<x<0
(2)0<a<3
【解析】解:(1.)由图象得: 不等式ax+b> ![]() 的解集为:x>1或﹣3<x<0;
的解集为:x>1或﹣3<x<0;
(2.)x2+a﹣ ![]() <0,
<0,
x2+a< ![]() ,
,
画函数y= ![]() 和y=x2的图象,
和y=x2的图象,
∵关于x的不等式x2+a﹣ ![]() <0(a>0)只有一个整数解,
<0(a>0)只有一个整数解,
∴整数解为x=1,
当x=1时,x2+a﹣ ![]() =0,
=0,
a=3,
∴0<a<3,
所以答案是:0<a<3.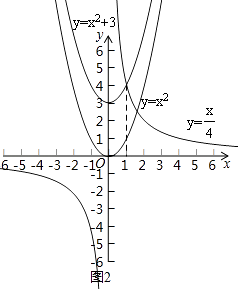

练习册系列答案
相关题目