ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋČôČÎŌâŌŧļöīúĘýĘ―ĢŽÔÚļøķĻĩÄ·ķΧÄÚĮóĩÃĩÄŨîÖĩĮĄšÃŌēÔÚļ÷ķΧÄÚĢŽÔōģÆÕâļöīúĘýĘ―ĘĮÕâļö·ķΧĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪĀýČįĢšđØÓÚ![]() ĩÄīúĘýĘ―
ĩÄīúĘýĘ―![]() ĢŽĩą
ĢŽĩą![]() ĘąĢŽīúĘýĘ―
ĘąĢŽīúĘýĘ―![]() ÔÚ
ÔÚ![]() ĘąÓÐŨîīóÖĩĢŽŨîīóÖĩΊ1ĢŧÔÚ
ĘąÓÐŨîīóÖĩĢŽŨîīóÖĩΊ1ĢŧÔÚ![]() ĘąÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ0ĢŽīËĘąŨîÖĩ1ĢŽ0ūųÔÚ
ĘąÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ0ĢŽīËĘąŨîÖĩ1ĢŽ0ūųÔÚ![]() ĢĻšŽķËĩãĢĐÕâļö·ķΧÄÚĢŽÔōģÆīúĘýĘ―
ĢĻšŽķËĩãĢĐÕâļö·ķΧÄÚĢŽÔōģÆīúĘýĘ―![]() ĘĮ
ĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĢĻ1ĢĐČôđØÓÚ![]() ĩÄīúĘýĘ―
ĩÄīúĘýĘ―![]() ĢŽĩą
ĢŽĩą![]() ĘąĢŽČĄĩÃĩÄŨîīóÖĩΊ________ĢŧŨîÐĄÖĩΊ________ĢŧīúĘýĘ―
ĘąĢŽČĄĩÃĩÄŨîīóÖĩΊ________ĢŧŨîÐĄÖĩΊ________ĢŧīúĘýĘ―![]() ________ĢĻĖĘĮĄąŧōĄ°ēŧĘĮĄąĢĐ
________ĢĻĖĘĮĄąŧōĄ°ēŧĘĮĄąĢĐ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŧ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŧ
ĢĻ2ĢĐŌÔÏÂđØÓÚ![]() ĩÄīúĘýĘ―ĢŽĘĮ
ĩÄīúĘýĘ―ĢŽĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĩÄĘĮ________Ģŧ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĩÄĘĮ________Ģŧ
ĒŲ![]() ĢŧĒÚ
ĢŧĒÚ![]() ĢŧĒÛ
ĢŧĒÛ![]() Ģŧ
Ģŧ
ĢĻ3ĢĐČôđØÓÚ![]() ĩÄīúĘýĘ―
ĩÄīúĘýĘ―![]() ĘĮ
ĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŽÔō
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŽÔō![]() ĩÄÖĩĘĮ________Ģŧ
ĩÄÖĩĘĮ________Ģŧ
ĢĻ4ĢĐČôđØÓÚ![]() ĩÄīúĘýĘ―
ĩÄīúĘýĘ―![]() ĘĮ
ĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŽĮó
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŽĮó![]() ĩÄŨîīóÖĩšÍŨîÐĄÖĩĢŪ
ĩÄŨîīóÖĩšÍŨîÐĄÖĩĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐ3ĢŽ0ĢŽēŧĘĮ ĢĻ2ĢĐĒÚ ĢĻ3ĢĐ![]() ĢĻ4ĢĐ
ĢĻ4ĢĐ![]() ĩÄŨîīóÖĩΊ4šÍŨîÐĄÖĩΊ0ĢŪ
ĩÄŨîīóÖĩΊ4šÍŨîÐĄÖĩΊ0ĢŪ
Ąū―âÎöĄŋ
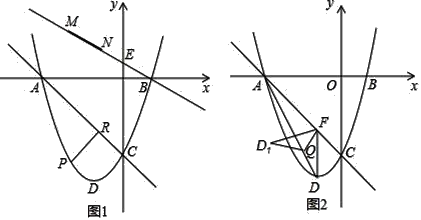
ĢĻ1ĢĐĮóģöīúĘýĘ―ĩÄŨîīóÖĩšÍŨîÐĄÖĩĢŽÔŲļųūÝÓŅšÃīúĘýĘ―ĩÄķĻŌå―øÐÐÅÐķÏžīŋÉĢŧ
ĢĻ2ĢĐļųūÝÓŅšÃīúĘýĘ―ĩÄķĻŌåķÔļũīúĘýĘ――øÐÐĮó―âžīŋÉĢŧ
ĢĻ3ĢĐ·ÖČýÖÖĮéŋö―øÐÐĮó―âĢšĒŲ![]() ĢŧĒÚ
ĢŧĒÚ![]() ĢŧĒÛ
ĢŧĒÛ![]() ĢŽžīŋÉĮóģömĩÄÖĩĢŧ
ĢŽžīŋÉĮóģömĩÄÖĩĢŧ
ĢĻ4ĢĐ·ÖČýÖÖĮéŋö―øÐÐĮó―âĢšĒŲ![]() ĢŧĒÚ
ĢŧĒÚ![]() ĢŧĒÛ
ĢŧĒÛ![]() ĢŽ―âĩÃ
ĢŽ―âĩÃ![]() ĢŽžīŋÉĮóģö
ĢŽžīŋÉĮóģö![]() ĩÄŨîīóÖĩšÍŨîÐĄÖĩĢŪ
ĩÄŨîīóÖĩšÍŨîÐĄÖĩĢŪ
ĢĻ1ĢĐĄß![]()
Ąāĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ3Ģŧĩą
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ3Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ0
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ0
Ąā![]() ĢŽ
ĢŽ![]()
đĘīúĘýĘ―![]() ēŧĘĮ
ēŧĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĢĻ2ĢĐĒŲĄßĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ3Ģŧĩą
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ3Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-1ĢŽ
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-1ĢŽ
Ąā![]() ĢŽ
ĢŽ![]()
Ąā![]() ēŧĘĮ
ēŧĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĒÚĄßĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ2Ģŧĩą
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ2Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-2ĢŽ
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-2ĢŽ
Ąā![]() ĢŽ
ĢŽ![]()
Ąā![]() ĘĮ
ĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĒÛĄßĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ2Ģŧĩą
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ2Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-4ĢŽ
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-4ĢŽ
Ąā![]() ĢŽ
ĢŽ![]()
Ąā![]() ēŧĘĮ
ēŧĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĢŪ
đĘĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĩÄĘĮĒÚĢŪ
ĩÄĄ°ÓŅšÃīúĘýĘ―ĄąĩÄĘĮĒÚĢŪ
ĢĻ3ĢĐĄßđØÓÚ![]() ĩÄīúĘýĘ―
ĩÄīúĘýĘ―![]() ĘĮ
ĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―Ąą
ĩÄĄ°ÓŅšÃīúĘýĘ―Ąą
Ąā·ÖŌÔÏÂČýÖÖĮéŋö―øÐÐĖÖÂÛĢš
ĒŲ![]()
![]()
Ąāĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ4Ģŧĩą
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ4Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ![]() ĢŽ
ĢŽ
Ąā![]()
ĄāēŧģÉÁĒ
ĒÚ![]()
![]()
Ąā![]() ĢŽ
ĢŽ![]()
Ąā![]()
―âĩÃ![]()
Ąāĩą![]() ģÉÁĒ
ģÉÁĒ
ĒÛ![]()
![]()
Ąāĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ![]() Ģŧĩą
Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-4ĢŽ
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ-4ĢŽ
Ąß![]()
ĄāēŧģÉÁĒ
đĘ![]() ĩÄÖĩĘĮ
ĩÄÖĩĘĮ![]() ĢŪ
ĢŪ
ĢĻ4ĢĐĄßđØÓÚ![]() ĩÄīúĘýĘ―
ĩÄīúĘýĘ―![]() ĘĮ
ĘĮ![]() ĩÄĄ°ÓŅšÃīúĘýĘ―Ąą
ĩÄĄ°ÓŅšÃīúĘýĘ―Ąą
Ąā·ÖŌÔÏÂČýÖÖĮéŋö―øÐÐĖÖÂÛ
ĒŲ![]()
ĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ![]() Ģŧĩą
Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ![]() ĢŽ
ĢŽ
Ąā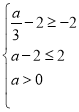
―âĩÃ![]()
ĒÚ![]()
![]()
Ąß![]()
Ąā![]() ĘąģÉÁĒ
ĘąģÉÁĒ
ĒÛ![]()
ĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ
ÓÐŨîīóÖĩĢŽŨîīóÖĩΊ![]() Ģŧĩą
Ģŧĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ
ÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊ![]() ĢŽ
ĢŽ
Ąā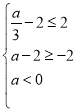
ÎÞ―â
Ąā![]()
Ąā![]() ĩÄŨîīóÖĩΊ4šÍŨîÐĄÖĩΊ0ĢŪ
ĩÄŨîīóÖĩΊ4šÍŨîÐĄÖĩΊ0ĢŪ

 žĪŧî˞ΎÓÅžÓŋÎĖÃÏĩÁÐīð°ļ
žĪŧî˞ΎÓÅžÓŋÎĖÃÏĩÁÐīð°ļ ŧîÁĶĘÔūíÏĩÁÐīð°ļ
ŧîÁĶĘÔūíÏĩÁÐīð°ļ