题目内容
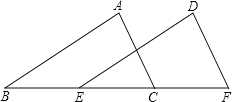
【题目】如图1所示,在![]() 中,
中,![]() ,点
,点![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,点
,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为斜边作等腰
为斜边作等腰![]() ,连接
,连接![]() ,
,![]() 满是条件
满是条件![]() .
.

(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(2)求证:![]() ;
;
(3)如图2,点![]() 是线段
是线段![]() 延长线上一点,其余条件与题干一致,探究
延长线上一点,其余条件与题干一致,探究![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
【答案】(1)AB=4;(2)见详解;(3)AE+AF=BC,证明见详解.
【解析】
(1)在等腰直角三角形DEF中,∠DEF=90°,求得∠1=20°,根据余角的定义得到∠2=∠DEF-∠1=70°,根据三角形的内角和得到∠3=60°,∠4=30°根据三角函数的定义得到AB=2BC,于是得到结论;
(2)如图1,过D作DM⊥AE于D,在△DEM中,由余角的定义得到∠2+∠5=90°,由于∠2+∠1=90°,推出∠1=∠5证得△DEM≌△EFA,根据全等三角形的性质得到AF=EM,根据三角形的内角和和余角的定义得到∠3=∠B,推出△DAM≌△ABC,根据全等三角形的性质得到BC=AM,即可得到结论;
(3)如图2,过D作DM⊥AE交AE的延长线于M根据余角的定义和三角形的内角和得到∠2=∠B,证得△ADM≌△BAC,由全等三角形的性质得到BC=AM,由于EF=DE,∠DEF=90°,推出∠4=∠5,证得△MED≌△AFE,根据全等三角形的性质得到ME=AF,即可得到结论.
解:(1)在等腰直角三角形DEF中,∠DEF=90°,

∵∠1=20°,
∴∠2=∠DEF![]() ∠1=70°,
∠1=70°,
∵∠EDA+∠2+∠3=180°,
∴∠3=60°,
∵EA⊥AB,
∴∠EAB=90°,
∵∠3+∠EAB+∠4=180°,
∴∠4=30°,
∵∠C=90°,
∴AB=2BC=4;
(2)如图1,过D作DM⊥AE于M,

在△DEM中,∠2+∠5=90°,
∵∠2+∠1=90°,
∴∠1=∠5,
∵DE=FE,
在△DEM与△EFA中,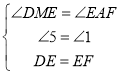 ,
,
∴△DEM≌△EFA,
∴AF=EM,
∵∠4+∠B=90°,
∵∠3+∠EAB+∠4=180°,
∴∠3+∠4=90°,
∴∠3=∠B,
在△DAM与△ABC中, ,
,
∴△DAM≌△ABC,
∴BC=AM,
∴AE=EM+AM=AF+BC;
(3)如图2,过D作DM⊥AE交AE的延长线于M,

∵∠C=90°,
∴∠1+∠B=90°,
∵∠2+∠MAB+∠1=180°,∠MAB=90°,
∴∠2+∠1=90°,∠2=∠B,
在△ADM与△BAC中,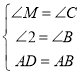 ,
,
∴△ADM≌△BAC,
∴BC=AM,
∵EF=DE,∠DEF=90°,
∵∠3+∠DEF+∠4=180°,
∴∠3+∠4=90°,
∵∠3+∠5=90°,
∴∠4=∠5,
在△MED与△AFE中, ,
,
∴△MED≌△AFE,
∴ME=AF,
∴AE+AF=AE+ME=AM=BC,
即AE+AF=BC.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案