题目内容
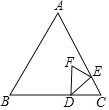
【题目】如图，等边△ABC中，AB＝6，点D在BC上，BD＝4，点E从点C出发，以每秒1个单位长度的速度沿CA方向向点A运动，△CDE关于DE的轴对称图形为△FDE．
（1）当t为何值时，点F在线段AC上．
（2）当0＜t＜4时，求∠AEF与∠BDF的数量关系；
（3）当点B、E、F三点共线时，求证：点F为线段BE的中点．
【答案】（1）t＝1s；（2）当0＜t≤1时，∠BDF﹣∠AEF＝120°；当1＜t＜4时，∠BDF+∠AEF＝120°；（3）详见解析．
【解析】
（1）由折叠的性质可得DF＝DC，EF＝EC，可证△DCF是等边三角形，可求CE的长，即可求解；
（2）分两种情况讨论，由折叠的性质和四边形内角和定理可求解；
（3）过点D作DG⊥EF于点G，过点E作EH⊥CD于点H，由勾股定理可求BG的长，通过证明△BGD∽△BHE，可求EC的长，即可得结论．
解：（1）∵△ABC是等边三角形
∴∠A＝∠B＝∠C＝60°
∵△CDE关于DE的轴对称图形为△FDE，
∴DF＝DC，EF＝EC，且点F在AC上，∠C＝60°，
∴△DCF是等边三角形，
∴CD＝CF＝AB﹣BD＝2，
∴CE＝1，
∴t＝
＝1s；
（2）如图1，当0＜t≤1时，
∵△CDE关于DE的轴对称图形为△FDE，
∴∠F＝∠C＝60°，∠FDE＝∠CDE，∠CED＝∠FED，
∵∠C+∠CDE+∠CED＝180°，
∴∠C+∠F+∠CDE+∠EDF+∠CED+∠FED＝360°，
∴∠CDF+180°+∠AEF＝360°﹣120°
∴180°﹣∠BDF+180°+∠AEF＝240°，
∴∠BDF﹣∠AEF＝120°；
如图2，当1＜t＜4时，
∵△CDE关于DE的轴对称图形为△FDE，
∴∠F＝∠C＝60°，∠FDE＝∠CDE，∠CED＝∠FED，
∵∠FDC+∠C+∠F+∠CEF＝360°，
∴180°﹣∠BDF+120°+180°﹣∠AEF＝360°，
∴∠BDF+∠AEF＝120°；
（3）如图3，过点D作DG⊥EF于点G，过点E作EH⊥CD于点H，
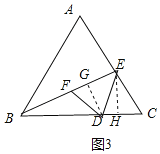
∵△CDE关于DE的轴对称图形为△FDE
∴DF＝DC＝2，∠EFD＝∠C＝60°，EF＝EC，
∵GD⊥EF，∠EFD＝60°
∴FG＝1，DG＝
FG＝，
∵BD2＝BG2+DG2，
∴16＝3+（BF+1）2，
∴BF＝
∴BG＝
，
∵EH⊥BC，∠C＝60°
∴CH＝
，EH＝HC＝
EC，
∵∠GBD＝∠EBH，∠BGD＝∠BHE＝90°
∴△BGD∽△BHE，
∴
,
∴
，
∴EC＝﹣1，
∴EC＝EF＝BF＝﹣1，
∴点F是线段BE的中点．
