题目内容
【题目】为支持大学生勤工俭学,市政府向某大学生提供了![]() 万元的无息贷款用于销售某种自主研发的产品,并约定该学生用经营的利润逐步偿还无息贷款,已知该产品的生产成本为每件
万元的无息贷款用于销售某种自主研发的产品,并约定该学生用经营的利润逐步偿还无息贷款,已知该产品的生产成本为每件![]() 元.每天还要支付其他费用
元.每天还要支付其他费用![]() 元.该产品每天的销售量
元.该产品每天的销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 关系为
关系为![]() .
.
(1)设每天的利润为![]() 元,当销售单价定为多少元时,每天的利润最大?最大利润为多少元?
元,当销售单价定为多少元时,每天的利润最大?最大利润为多少元?![]() 注:每天的利润
注:每天的利润![]() 每天的销售利润一每天的支出费用
每天的销售利润一每天的支出费用![]()
(2)若销售单价不得低于其生产成本,且销售每件产品的利润率不能超过![]() ,则该学生最快用多少天可以还清无息贷款?
,则该学生最快用多少天可以还清无息贷款?
【答案】(1)当销售单价定为25元时,日销售利润最大为200元;(2)该生最快用100天可以还清无息贷款.
【解析】
(1)计算利润![]() =销量×每件的利润-支付的费用,化为顶点式,可得结论;
=销量×每件的利润-支付的费用,化为顶点式,可得结论;
(2)先得出每日利润的最大值,即可求解.
(1)![]()
![]()
![]()
∵![]() <0,
<0,
∴当x=25时,日利润最大,为200元,
∴当销售单价定为25元时,日销售利润最大为200元;
(2) 由题意得: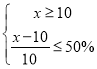 ,
,
解得:![]() ,
,
![]() ,
,
∵![]() <0,
<0,
∴抛物线开口向下,当![]() 时,
时,![]() 随
随![]() 的值增大而增大,
的值增大而增大,
∴当x=15时,日利润最大为![]() 100元,
100元,
∵10000![]() 100=100,
100=100,
∴该生最快用100天可以还清无息贷款.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校九年级(1)班甲、乙两名同学在5次引体向上测试中的有效次数如下:
甲:8,8,7,8,9.乙:5,9,7,10,9.
甲、乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 |
| 8 | 0.4 |
乙 |
| 9 |
| 3.2 |
根据以上信息,回答下列问题:
(1)表格中![]() _______,
_______,![]() _______,
_______,![]() _______.(填数值)
_______.(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是_______________________________________.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是_______________________________________.
(3)乙同学再做一次引体向上,次数为n,若乙同学6次引体向上成绩的中位数不变,请写出n的最小值.