题目内容
【题目】在平面直角坐标系xOy中,M为直线l:x=a上一点,N是直线l外一点,且直线MN与x轴不平行,若MN为某个矩形的对角线,且该矩形的边均与某条坐标轴垂直,则称该矩形为直线l的“伴随矩形”.如图为直线l的“伴随矩形”的示意图.

(1)已知点A在直线l:x=2上,点B的坐标为(3,﹣2)
①若点A的纵坐标为0,则以AB为对角线的直线l的“伴随矩形”的面积是 ;
②若以AB为对角线的直线l的“伴随矩形”是正方形,求直线AB的表达;
(2)点P在直线l:x=m上,且点P的纵坐标为4,若在以点(2,1),(﹣2,1),(﹣2,﹣1),(2,﹣1)为顶点的四边形上存在一点Q,使得以PQ为对角线的直线l的“伴随矩形”为正方形,直接写出m的取值范围.
【答案】(1)①以AB为对角线的直线l的“伴随矩形”AMBN的面积为2;②直线AB的表达式为y=﹣x+1或y=x﹣5;(2)m的范围为﹣7≤m≤﹣1或1≤m≤7.
【解析】
(1)①根据“伴随矩形”的定义画出图形即可解决问题;
②根据题意,当以AB为对角线的直线l的“伴随矩形”为正方形时,点A的坐标为(2,-1)或(2,-3),利用待定系数法即可解决问题;
(2)如图3中,求出经过特殊位置时当P坐标即可解决问题:当Q1坐标为(-2,-1)时,可得P1(-7,4);当Q2坐标为(2,1)时,可得P2(-14);当Q3坐标为(2,-1)时,可得P3(7,4);当Q4坐标为(-2,1)时,可得P4(1,4);再结合图象即可解决问题;
(1)①如图1中,∵A(2,0),B(3,﹣2).
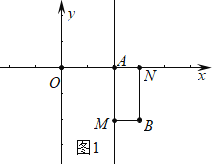
∴以AB为对角线的直线l的“伴随矩形”AMBN的面积=1×2=2.
②如图2中,
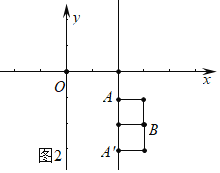
根据题意,当以AB为对角线的直线l的“伴随矩形”为正方形时,
点A的坐标为(2,﹣1)或(2,﹣3).
可得,直线AB的表达式为:y=﹣x+1或y=x﹣5.
(2)如图3中,
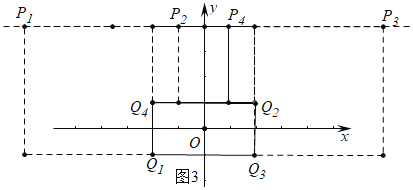
当Q1坐标为(﹣2,﹣1)时,可得P1(﹣7,4);
当Q2坐标为(2,1)时,可得P2(﹣14);
当Q3坐标为(2,﹣1)时,可得P3(7,4);
当Q4坐标为(﹣2,1)时,可得P4(1,4);
观察图象可知:在以点(2,1),(﹣2,1),(﹣2,﹣1),(2,﹣1)为顶点的四边形上存在一点Q,使得以PQ为对角线的直线l的“伴随矩形”为正方形时,m的范围为﹣7≤m≤﹣1或1≤m≤7.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案