题目内容
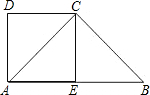 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=| 1 | 2 |
(1)求证:四边形AECD是正方形;
(2)求∠B的度数.
分析:(1)根据E是AB的中点,得AE=BE,因为AB∥DC,所以四边形AECD是平行四边形,而∠DAB=90°,所以四边形AECD是矩形,又因为AD=CD,所以四边形AECD是正方形;
(2)根据(1)得到∠CAE=45°,而E是AB的中点,CE⊥AE,所以CE是AB的垂直平分线,最后∠B的度数就可求.
(2)根据(1)得到∠CAE=45°,而E是AB的中点,CE⊥AE,所以CE是AB的垂直平分线,最后∠B的度数就可求.
解答:(1)证明:∵E是AB的中点,
∴AE=
AB=DC,(1分)
∵AB∥DC,
∴AE∥DC,
∴四边形AECD是平行四边形,(3分)
∵∠DAE=90°,
∴平行四边形AECD是矩形,(4分)
∵AD=DC,
∴矩形AECD是正方形.(5分)
(2)解:∵四边形AECD是正方形,
∴∠CAE=45°,(6分)
∵E是AB的中点,CE⊥AE,
∴CE垂直平分AB,
∴△ACB是等腰三角形,(7分)
∴∠B=∠CAE=45°(8分)
∴AE=
| 1 |
| 2 |
∵AB∥DC,
∴AE∥DC,
∴四边形AECD是平行四边形,(3分)
∵∠DAE=90°,
∴平行四边形AECD是矩形,(4分)
∵AD=DC,
∴矩形AECD是正方形.(5分)
(2)解:∵四边形AECD是正方形,
∴∠CAE=45°,(6分)
∵E是AB的中点,CE⊥AE,
∴CE垂直平分AB,
∴△ACB是等腰三角形,(7分)
∴∠B=∠CAE=45°(8分)
点评:此题考查正方形的性质及判定方法等的综合运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,△A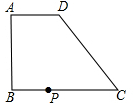 PD中边AP上的高为( )
PD中边AP上的高为( )
 PD中边AP上的高为( )
PD中边AP上的高为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
 结论是否成立?请说明理由.
结论是否成立?请说明理由. 已知直角梯形ABCD如图放置在平面直角坐标系中,∠DCB=30°,AB边在y轴上,点D的横坐标为6,CQ⊥x轴,垂足为Q,点Q的横坐标为12,过CD的直线l交x轴于点E,E点坐标为(18,0).
已知直角梯形ABCD如图放置在平面直角坐标系中,∠DCB=30°,AB边在y轴上,点D的横坐标为6,CQ⊥x轴,垂足为Q,点Q的横坐标为12,过CD的直线l交x轴于点E,E点坐标为(18,0).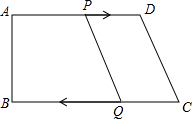 C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t.
C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t.