Question

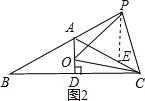
【题目】如图，等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线一点，点O是线段AD上一点，OP=OC．
（1）已知∠APO=18°，求∠DCO的度数；
（2）求证：△OPC是等边三角形；
（3）求证：AC=AO+AP．

Answer 1

【答案】（1）12°；（2）见解析；（3）见解析

【解析】

（1）利用等边对等角，即可证得：∠APO=∠ABO，∠DCO=∠DBO，则∠APO+∠DCO=∠ABO+∠DBO=∠ABD，据此即可求解；
（2）证明∠POC=60°且OP=OC，即可证得△OPC是等边三角形；
（3）首先证明△OPA≌△CPE，则AO=CE，AC=AE+CE=AO+AP．

（1）解：如图1，连接OB，

∵AB=AC，AD⊥BC，
∴BD=CD，∠BAD=∠BAC=×120°=60°，
∴OB=OC，∠ABC=90°-∠BAD=30°
∵OP=OC，
∴OB=OC=OP，
∴∠APO=∠ABO，∠DCO=∠DBO，
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°；
∴∠DCO=30°-∠APO=30°-18°=12°；
（2）证明：∵∠APC+∠DCP+∠PBC=180°，
∴∠APC+∠DCP=150°，
∵∠APO+∠DCO=30°，
∴∠OPC+∠OCP=120°，
∴∠POC=180°-（∠OPC+∠OCP）=60°，
∵OP=OC，
∴△OPC是等边三角形；
（3）证明：如图2，在AC上截取AE=PA

，
∵∠PAE=180°-∠BAC=60°，
∴△APE是等边三角形，
∴∠PEA=∠APE=60°，PE=PA，
∴∠APO+∠OPE=60°，
∵∠OPE+∠CPE=∠CPO=60°，
∴∠APO=∠CPE，
∵OP=CP，
在△OPA和△CPE中，

，
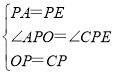∴△OPA≌△CPE（SAS），
∴AO=CE，
∴AC=AE+CE=AO+AP．