题目内容
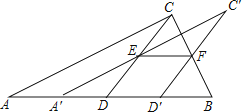
【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF =AD;
(2)若AD=2,AB=8,当BC为多少时,点B在线段AF的垂直平分线上?说明理由.

【答案】(1)证明见解析;(2)BC为6时,点B在线段AF的垂直平分线上;
【解析】
(1)通过求证△FEC≌△AED来证明CF=AD;
(2)若点B在线段AF的垂直平分线上,则应有AB=BF∵AB=8,CF=AD=2,∴BC=BF-CF=8-2=6时有AB=BF.
(1)证明:∵E是CD的中点
∴DE=CE
∵AD∥BC
∴∠D=∠ECF,∠DAE=∠EFC
∴△ADE≌△FCE

∴CF=DA
(2)BC=6;
理由如下:连接BE
∵BE垂直平分AF
∴AB=BF
由(1)得AD=CF
∵AD=2,AB=8
∴BC=BF-CF
=AB-AD
=8-2
=6
∴当BC为6时,点B在线段AF的垂直平分线上

练习册系列答案
相关题目
【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
体育锻炼时间 | 人数 |
4≤x≤6 | |
2≤x<4 | 43 |
0≤x<2 | 15 |
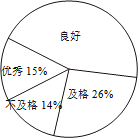
(1)试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;
(2)统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为x小时);
(3)全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.