题目内容
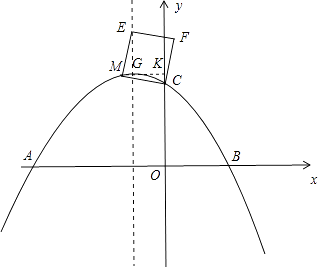
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC= ![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
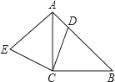
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵C(0,3),
∴OC=3,
∵tan∠OAC= ![]() ,
,
∴OA=4,
∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入y=ax2+2ax+c中,
得 ![]() ,解得:
,解得: 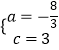 ,
,
∴抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+3
x+3
(2)
解:设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,3)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴直线AC的解析式为y= ![]() x+3.
x+3.
设N(x,0)(﹣4<x<0),则H(x, ![]() x+3),P(x,﹣
x+3),P(x,﹣ ![]() x2﹣
x2﹣ ![]() x+3),
x+3),
∴PH=﹣ ![]() x2﹣
x2﹣ ![]() x+3﹣(
x+3﹣( ![]() x+3)=﹣
x+3)=﹣ ![]() x2﹣
x2﹣ ![]() x=﹣
x=﹣ ![]() (x+2)2+
(x+2)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴PH有最大值,
当x=﹣2时,PH取最大值,最大值为 ![]()
(3)
解:过点M作MK⊥y轴于点K,交对称轴于点G,则∠MGE=∠MKC=90°,
∴∠MEG+∠EMG=90°,
∵四边形CMEF是正方形,
∴EM=MC,∠MEC=90°,
∴∠EMG+∠CMK=90°,
∴∠MEG=∠CMK.
在△MCK和△MEG中, 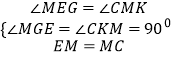 ,
,
∴△MCK≌△MEG(AAS),
∴MG=CK.
由抛物线的对称轴为x=﹣1,设M(x,﹣ ![]() x2﹣
x2﹣ ![]() x+3),则G(﹣1,﹣
x+3),则G(﹣1,﹣ ![]() x2﹣
x2﹣ ![]() x+3),K(0,﹣
x+3),K(0,﹣ ![]() x2﹣
x2﹣ ![]() x+3),
x+3),
∴MG=|x+1|,CK=|﹣ ![]() x2﹣
x2﹣ ![]() x+3﹣3|=|﹣
x+3﹣3|=|﹣ ![]() x2﹣
x2﹣ ![]() x|=|
x|=| ![]() x2+
x2+ ![]() x|,
x|,
∴|x+1|=| ![]() x2+
x2+ ![]() x|,
x|,
∴ ![]() x2+
x2+ ![]() x=±(x+1),
x=±(x+1),
解得:x1=﹣4,x2=﹣ ![]() ,x3=﹣
,x3=﹣ ![]() ,x4=2,
,x4=2,
代入抛物线解析式得:y1=0,y2= ![]() ,y3=
,y3= ![]() ,y4=0,
,y4=0,
∴点M的坐标是(﹣4,0),(﹣ ![]() ,
, ![]() ),(﹣
),(﹣ ![]() ,
, ![]() )或(2,0).
)或(2,0).
【解析】(1)由点C的坐标以及tan∠OAC= ![]() 可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.本题考查了待定系数法求函数解析式、二次函数的性质、正方形的性质以及全等三角形的判定与性质,解题的关键是:(1)利用待定系数法求出抛物线解析式;(2)根据二次函数的性质解决最值问题;(3)根据正方形的性质得出关于x的含绝对值符号的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出关于x的含绝对值符号的一元二次方程,解方程求出点的横坐标是关键.
可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.本题考查了待定系数法求函数解析式、二次函数的性质、正方形的性质以及全等三角形的判定与性质,解题的关键是:(1)利用待定系数法求出抛物线解析式;(2)根据二次函数的性质解决最值问题;(3)根据正方形的性质得出关于x的含绝对值符号的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出关于x的含绝对值符号的一元二次方程,解方程求出点的横坐标是关键.
【考点精析】通过灵活运用二次函数的性质和正方形的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.

 名校课堂系列答案
名校课堂系列答案