题目内容
已知抛物线y=mx2-(m-5)x-5(m>0)与x轴交于两点A(x1,0)、B(x2,0)(x1<x2),与y轴交于点C,且AB=6.
(1)求抛物线和直线BC的解析式;
(2)在给定的直角坐标系中,画出抛物线和直线BC;
(3)若⊙P过A、B、C三点,求⊙P的半径;
(4)抛物线上是否存在点M,过点M作MN⊥x轴于点N,使△MBN被直线BC分成面积比为1:3的两部分?若存在,请求出点M的坐标;若不存在,请说明理由.

(1)求抛物线和直线BC的解析式;
(2)在给定的直角坐标系中,画出抛物线和直线BC;
(3)若⊙P过A、B、C三点,求⊙P的半径;
(4)抛物线上是否存在点M,过点M作MN⊥x轴于点N,使△MBN被直线BC分成面积比为1:3的两部分?若存在,请求出点M的坐标;若不存在,请说明理由.

(1)由题意得:x1+x2=
,x1•x2=
,x2-x1=6
则(x1+x2)2-4x1x2=36,(
)2+
=36
解得:m1=1,m2=-
.
经检验m=1,
∴抛物线的解析式为:y=x2+4x-5
或:由mx2-(m-5)x-5=0得,x=1或x=-
∵m>0,
∴1-
=6,
∴m=1.
∴抛物线的解析式为y=x2+4x-5
由x2+4x-5=0得x1=-5,x2=1
∴A(-5,0),B(1,0),C(0,-5).
设直线BC的解析式为y=kx+b,
则
∴
∴直线BC的解析式为y=5x-5;
(2)如图1;
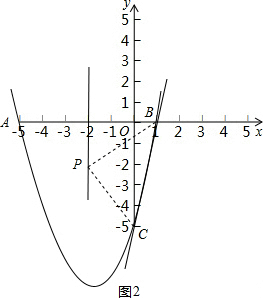
(3)如图2,由题意,圆心P在AB的中垂线上,即在抛物线y=x2+4x-5的对称轴直线x=-2上,
设P(-2,-h)(h>0),(6分)
连接PB、PC,则PB2=(1+2)2+h2,PC2=(5-h)2+22,
由PB2=PC2,
即(1+2)2+h2=(5-h)2+22,解得h=2.
∴P(-2,-2),
∴⊙P的半径PB=
=
;
(4)如图3,设MN交直线BC于点E,点M的坐标为(t,t2+4t-5),则点E的坐标为(t,5t-5).
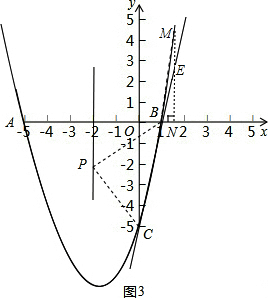 若S△MEB:S△ENB=1:3,则ME:EN=1:3.
若S△MEB:S△ENB=1:3,则ME:EN=1:3.
∴EN:MN=3:4,
∴t2+4t-5=
(5t-5).
解得t1=1(不合题意舍去),t2=
,
∴M(
,
).
若S△MEB:S△ENB=3:1,则ME:EN=3:1.
∴EN:MN=1:4,
∴t2+4t-5=4(5t-5).
解得t3=1(不合题意舍去),t4=15,
∴M(15,280).
∴存在点M,点M的坐标为(
,
)或(15,280).
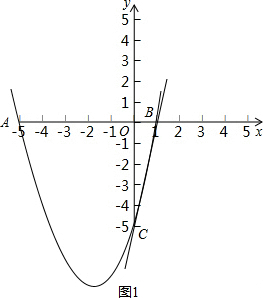
| m-5 |
| m |
| -5 |
| m |
则(x1+x2)2-4x1x2=36,(
| m-5 |
| m |
| 20 |
| m |
解得:m1=1,m2=-
| 5 |
| 7 |
经检验m=1,
∴抛物线的解析式为:y=x2+4x-5
或:由mx2-(m-5)x-5=0得,x=1或x=-
| 5 |
| m |
∵m>0,
∴1-
| -5 |
| m |
∴m=1.
∴抛物线的解析式为y=x2+4x-5
由x2+4x-5=0得x1=-5,x2=1
∴A(-5,0),B(1,0),C(0,-5).
设直线BC的解析式为y=kx+b,
则
|
∴
|
∴直线BC的解析式为y=5x-5;
(2)如图1;
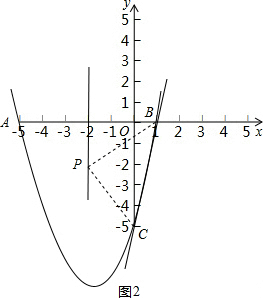
(3)如图2,由题意,圆心P在AB的中垂线上,即在抛物线y=x2+4x-5的对称轴直线x=-2上,
设P(-2,-h)(h>0),(6分)
连接PB、PC,则PB2=(1+2)2+h2,PC2=(5-h)2+22,
由PB2=PC2,
即(1+2)2+h2=(5-h)2+22,解得h=2.
∴P(-2,-2),
∴⊙P的半径PB=
| (1+2)2+22 |
| 13 |
(4)如图3,设MN交直线BC于点E,点M的坐标为(t,t2+4t-5),则点E的坐标为(t,5t-5).
 若S△MEB:S△ENB=1:3,则ME:EN=1:3.
若S△MEB:S△ENB=1:3,则ME:EN=1:3.∴EN:MN=3:4,
∴t2+4t-5=
| 4 |
| 3 |
解得t1=1(不合题意舍去),t2=
| 5 |
| 3 |
∴M(
| 5 |
| 3 |
| 40 |
| 9 |
若S△MEB:S△ENB=3:1,则ME:EN=3:1.
∴EN:MN=1:4,
∴t2+4t-5=4(5t-5).
解得t3=1(不合题意舍去),t4=15,
∴M(15,280).
∴存在点M,点M的坐标为(
| 5 |
| 3 |
| 40 |
| 9 |
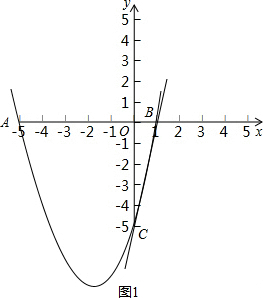

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




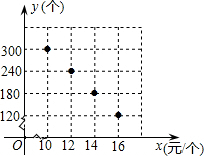 如图所示:
如图所示: