题目内容
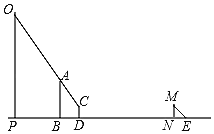
【题目】如图,笑笑和爸爸想要测量直立在地面上的建筑物OP与广告牌AB的高度.首先,笑笑站在离广告牌B处4米的D处看到广告牌AB的顶端A、建筑物OP的顶端O一条直线上;此时,在阳光下,爸爸站在N处,他的影长NE=2.1米,同一时刻,测得建筑物OP的影长为PG=28米,已知建筑物OP与广告牌AB之间的水平距离为11米,笑笑的眼睛到地面的距离CD=1.5米,爸爸的身高MN=1.8米.
(1)请你画出表示建筑物OP在阳光下的影子PG;
(2)求:①建筑物OP的高度;
②广告牌AB的高度.
【答案】(1)见解析,(2)①24;②7.5
【解析】
(1)根据同一时刻光线平行过点O作ME的平行线交PE于点G即可画出建筑物OP在阳光下的影子PG;
(2)①由△OPG∽△MNE,得物高比物高等于影长比影长列比例式求解即可;
②作CF⊥OP于点F,交AB于点H,证△OFC∽△AHC,得对应边成比例即可求得AB的长.
解:(1)如图:PG即为建筑物OP在阳光下的影子.
(2)①根据题意,得OP∥MN,OG∥ME,
∴∠OPG=∠MNE,∠OGP=∠MEN,
∴△OPG∽△MNE,
∴![]() ,即
,即![]() ,
,
解得OP=24.
答:建筑物OP的高度为24m.
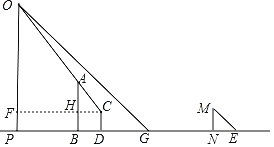
②过点C作CF⊥OP于点F,交AB于点H,
则∠OFC=∠AHC=90°,∠OCF=∠ACH,
FH=PB=11,HC=BD=4,CD=HB=FP=1.5,
则OF=OP﹣PF=24﹣1.5=22.5,FC=PD=PB+BD=15.
∴△OFC∽△AHC,
∴![]() ,即
,即![]() ,
,
解得AH=6.
∴AB=AH+BH=6+1.5=7.5.
答:广告牌AB的高度为7.5m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目