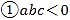题目内容
【题目】定义:如图![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在抛物线上(点
在抛物线上(点![]() 与
与![]() 两点不重合),如果
两点不重合),如果![]() 的三边满足
的三边满足![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() 的勾股点。
的勾股点。
(![]() )直接写出抛物线
)直接写出抛物线![]() 的勾股点的坐标;
的勾股点的坐标;
(![]() )如图
)如图![]() ,已知抛物线
,已知抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 的勾股点,求抛物线
的勾股点,求抛物线![]() 的函数表达式;
的函数表达式;
(![]() )在(
)在(![]() )的条件下,点
)的条件下,点![]() 在抛物线
在抛物线![]() 上,求满足条件
上,求满足条件![]() 的点
的点![]() (异于点
(异于点![]() )的坐标.
)的坐标.
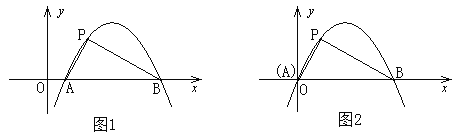
【答案】(1)![]() ;(2)
;(2)![]() ;(3)Q有3个:
;(3)Q有3个: ![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据抛物线勾股点的定义即可得;
(2)作PG⊥x轴,由点P坐标求得AG=1、PG=![]() 、PA=2,得到
、PA=2,得到![]() ,
,
从而求得AB=4,即B(4,0),待定系数法求解可得;
(3)由S△ABQ=S△ABP且两三角形同底,可知点Q到x轴的距离为![]() ,据此求解可得.
,据此求解可得.
解:
(1)抛物线![]() 的勾股点的坐标为
的勾股点的坐标为![]() ;
;
(2)抛物线![]() 过原点,即点
过原点,即点![]() ,如图,作
,如图,作![]() 轴于点G,
轴于点G,
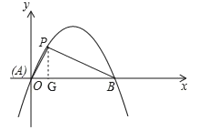
∵点P的坐标为![]() ,
,
∴![]()
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∴![]() ,
,![]() ,即点B的坐标为(4,0)
,即点B的坐标为(4,0)
∴不妨设抛物线解析式为![]() ,
,
将点![]() 代入得:
代入得: ![]() ,即抛物线解析式为
,即抛物线解析式为![]() .
.
(3)①当点Q在x轴上方时,由![]() 知点Q的纵坐标为
知点Q的纵坐标为![]() ,
,
则有![]() ,
,
计算得出: ![]() (与P点重合,不符合题意,舍去),
(与P点重合,不符合题意,舍去),
∴点Q的坐标为![]() ;
;
②当点Q在x轴下方时,由![]() 知点Q的纵坐标为
知点Q的纵坐标为![]() ,
,
则有![]() ,
,
计算得出: ![]() ,
,
∴点Q的坐标为![]() 或
或![]() ;
;
综上,满足条件的点Q有3个: ![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目