题目内容
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
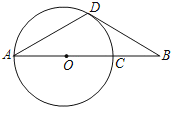
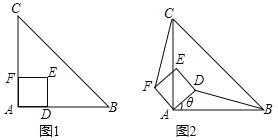
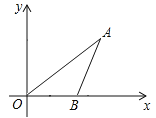
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
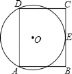
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.

【答案】(1)DF=![]() BE;(2)见解析;(3)
BE;(2)见解析;(3)![]() ;
;
【解析】
(1)证明△ACE≌△BCE,则AE=BE,DF是直角△ADE的中线,DF=![]() AE,即可证明DF=
AE,即可证明DF=![]() BE;
BE;
(2)连接AM,证明△ACM≌△BCE,则AM=BE,DF为△AME的中位线,DF=![]() =
=![]() BE;
BE;
(3)易知CD=DE=2,由勾股定理CE=![]() ,BE=CE—CB=
,BE=CE—CB=![]() ,DF=
,DF=![]() BE,可求得DF=
BE,可求得DF=![]() .
.
(1) ∵∠ACB=∠CDE=90°,AC=BC,CD =ED,
∴∠ACE=∠BCE=45°,
∴△ACE≌△BCE,
∴AE=BE,因为DF是直角△ADE的中线,
∴DF=![]() AE
AE
∴DF=![]() BE
BE
(2)如图,将△CDE沿着CD翻折,得到△DCM≌△DCE,连接AM,
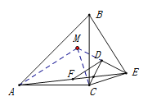
由△CDE为等腰直角三角形易知△CME为等腰直角三角形,
在△ACM和△BCE中,
AC=BC,∠ACM=∠BCE ,CM=CE,
∴△ACM≌△BCE,
∴AM=BE
∵F为AE的中点,D为ME的中点
∴DF为△AME的中位线,
∴DF=![]() ,
,
∴DF=![]() BE.
BE.
(3)将△EDC沿DC翻折得到△DCM
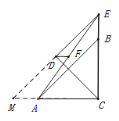
CD=DE=2,由勾股定理可知CE=![]()
BE=CE—CB=![]()
由前面的结论可知:DF=![]() BE
BE
∴DF=![]() .
.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
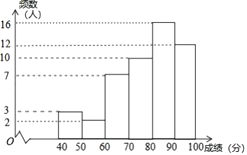
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.