题目内容
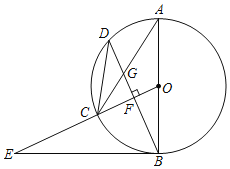
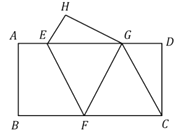
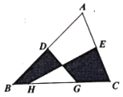
【题目】如图,D、E分别是△ABC的边AB、AC的中点,H、G是边BC上的点,且HG=![]() BC,S△ABC =12,则图中阴影部分的面积为( )
BC,S△ABC =12,则图中阴影部分的面积为( )
A.6B.4C.3D.2
【答案】A
【解析】
连接DE,作AF⊥BC于F,根据三角形中位线定理得出DE=![]() BC,DE∥BC,根据相似三角形的判定定理和性质定理,结合三角形面积计算即可.
BC,DE∥BC,根据相似三角形的判定定理和性质定理,结合三角形面积计算即可.
连接DE,作AF⊥BC于F,交DE于H,
∵D,E分别是AB,AC的中点,
∴DE=![]() BC,DE∥BC,AH=FH,
BC,DE∥BC,AH=FH,
∴△ADE∽△ABC,AH⊥DE,
∴△ADE的面积=![]() ,
,
∴四边形 DBCE的面积=12-3=9,
∵HG=![]() BC,
BC,
∴DE=HG,
∴△DOE的面积+△HOG的面积=![]() =△ADE的面积=3,
=△ADE的面积=3,
∴图中阴影部分的面积= 9- 3=6,
故选:A.

 名校课堂系列答案
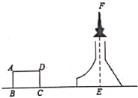
名校课堂系列答案【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
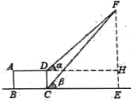
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
【题目】某社区组织了以“奔向幸福,‘毽’步如飞”为主题的踢毽子比赛活动,初赛结束后有甲、乙两个代表队进入决赛,已知每队有5名队员,按团体总数排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是两队各队员的比赛成绩.
1 号 | 2 号 | 3 号 | 4 号 | 5 号 | 总数 | |
甲队 | 103 | 102 | 98 | 100 | 97 | 500 |
乙队 | 97 | 99 | 100 | 96 | 108 | 500 |
经统计发现两队5名队员踢毽子的总个数相等,按照比赛规则,两队获得并列第一.学习统计知识后,我们可以通过考查数据中的其它信息作为参考,进行综合评定:
(1)甲、乙两队的优秀率分别为 ;
(2)甲队比赛数据的中位数为 个;乙队比赛数据的中位数为 个;
(3)分别计算甲、乙两队比赛数据的方差;
(4)根据以上信息,你认为综合评定哪一个队的成绩好?简述理由.