题目内容
【题目】如图,在矩形![]() 中,
中,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上两点,将矩形
上两点,将矩形![]() 沿
沿![]() 折叠后,
折叠后,![]() 点落在
点落在![]() 边上
边上![]() 点处,连接
点处,连接![]() ,若四边形
,若四边形![]() 为菱形,且
为菱形,且![]() ,则
,则![]() 四边形
四边形![]() ( )
( )
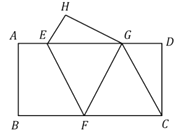
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过点F作FM⊥AD交AD于点M,由矩形及折叠可证得EG=FG,再由菱形EFCG可得EF=EG,进而可证得△EFG为等边三角形,利用AB=FM=![]() 可求得等边三角形的边长,在Rt△HEG中可求得EH的长也就是AE的长,最后利用梯形的面积公式计算即可.
可求得等边三角形的边长,在Rt△HEG中可求得EH的长也就是AE的长,最后利用梯形的面积公式计算即可.
解:如图,过点F作FM⊥AD交AD于点M,
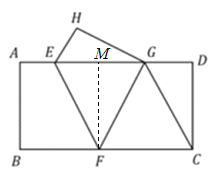
又∵在矩形ABCD中,∠A=∠B=90°,AD∥BC,
∴四边形ABFM为矩形,
∴FM=AB=![]() ,
,
∵AD∥BC,
∴∠BFE=∠GEF,
∵折叠,
∴∠BFE=∠GFE,
∴∠GEF =∠GFE,
∴GE =GF,
∵四边形![]() 为菱形,
为菱形,
∴GE =EF,
∴△GEF为等边三角形,
∴∠EGF=60°,
在Rt△FMG中,sin∠EGF=![]() ,
,
∴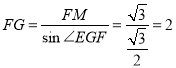
∴BF=FG=EG=2,
∵FG∥EH,
∴∠GEH=∠EGF=60°,
∵折叠,
∴∠H=∠B=90°,EH=AE,
在Rt△GEH中,cos∠GEH=![]() ,
,
∴EH=EG·cos∠GEH=2×![]() =1,
=1,
∴AE=1,
∴AG=AE+EG=1+2=3,
∴![]() 四边形
四边形![]()
![]() (AG+BF)·AB=
(AG+BF)·AB=![]() ×(3+2)×
×(3+2)×![]() =
=![]() ,
,
故选:B.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】为了了解初三学生的中考体育备考情况,西安铁一中分校体育组从初三年级全年级学生中随机抽取部分学生进行测试,现将从报排球项目所有女生中随机抽取到的60名女生的排球成绩(40秒内有效垫球个数)进行整理,得到下列图表中信息:
垫球个数 | 频数 |
|
|
| 4 |
|
|
| 26 |
| 10 |

请根据所给信息,解答下列问题:
(1)![]() __________,
__________,![]() __________;
__________;
(2)这60名学生垫球个数的中位数落在__________段;
(3)全校报考排球项目女生共有450人,根据以往的经验垫球个数在30个以上(包含30个)在中考中能取得良好以上成绩,请估计中考体育考试中女生排球项目达到良好以上的女生人数.