题目内容
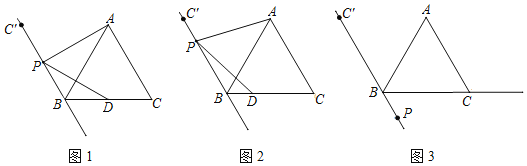
【题目】△ABC是等边三角形,点C关于AB对称的点为C′,点P是直线C′B上的一个动点,连接AP,作∠APD=60°交射线BC于点D.
(1)若点P在线段C′B上(不与点C′,点B重合)
①如图1,当点P是线段C′B的中点时,直接写出线段PD与线段PA的数量关系 .
②如图2,点P是线段C′B上任意一点,证明PD与PA的数量关系.
(2)若点P在线段C′B的延长线上,
①依题意补全图3;
②直接写出线段BD,AB,BP之间的数量关系为: .
【答案】(1)①PD=PA;②详见解析;(2)①详见解析;②BD=BP+AB.
【解析】
(1)①如图1中,连接AC′,可证△ABC′是等边三角形,由PB=PC′,推出PA⊥BC′,可求∠BDP=∠BPD=30°,可得PB=PD,由“SAS”可证△ABD≌△ABP,可得AP=AD,由等边三角形的性质可求解;
②如图2中,作∠BPE=60°交AB于点E,只要证明△PBD≌△PEA(ASA)即可解决问题;
(2)①根据要求画出图形即可解决问题;
②结论:BD=BP+AB.如图3中,在BD上取一点E,使得BE=PB.只要证明△BPA≌△EPD(SAS),即可解决问题.
(1)①解:如图1中,连接AC′.

∵△ABC是等边三角形,
∴∠ABC=60°,
∵点C'与点C关于AB对称,
∴∠C'BA=∠CBA=60°,BC′=BC=BA,
∴△ABC′是等边三角形,
∵PB=PC′,
∴PA⊥BC′,且∠APD=60°,
∴∠BPD=30°,且∠PBD=120°
∴∠BDP=∠BPD=30°,
∴PB=BD,且∠ABC=∠ABC'=60°,AB=AB,
∴△ABD≌△ABP(SAS)
∴AP=AD,且∠APD=60°,
∴△APD是等边三角形,
∴AP=PD,
故答案为AP=PD.
②证明:如图2中,作∠BPE=60°交AB于点E.
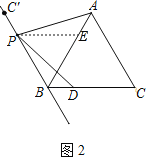
∵△ABC是等边三角形,
∴∠ABC=60°,
∵点C'与点C关于AB对称,
∴∠C'BA=∠CBA=60°=∠BPE,
∴∠PEB=60°.
∴△PBE是等边三角形,
∴PB=PE,AEP=120°=∠PBD.
∵∠BPD+∠DPE=60°,∠APE+∠DPE=60°,
∴∠BPD=∠APE,
在△PBD和△PEA中,

∴△PBD≌△PEA(ASA).
∴PD=PA.
(2)①解:补全图形,如图3所示:

②解:结论:BD=BP+AB.
理由:如图3中,在BD上取一点E,使得BE=PB.
∵∠EBP=60°,BE=BP,
∴△EBP是等边三角形,
由(1)可知:△PAD是等边三角形,
∴∠BPE=∠APD=60°,
∴∠APB=∠EPD,
∵PB=PE,PA=PD,
∴△BPA≌△EPD(SAS),
∴AB=DE,
∴BD=BE+ED=BP+AB.
故答案为BD=BP+AB.







