Question

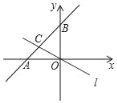
【题目】如图，已知直线y＝x+4与x轴、y轴交于A，B两点，直线l经过原点，与线段AB交于点C，并把△AOB的面积分为2：3两部分，求直线l的解析式．

Answer 1

【答案】y＝﹣x或y＝﹣x．

【解析】

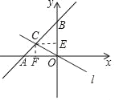
根据直线y＝x+4的解析式可求出A、B两点的坐标，当直线l把△ABO的面积分为S△AOC：S△BOC＝2：3时，作CF⊥OA于F，CE⊥OB于E，可分别求出△AOB与△AOC的面积，再根据其面积公式可求出两直线交点的坐标，从而求出其解析式；当直线l把△ABO的面积分为S△AOC：S△BOC＝2：3时，同（1）．

解：直线l的解析式为：y＝kx，

对于直线y＝x+4的解析式，当x＝0时，y＝4，y＝0时，x＝﹣4，

∴A（﹣4，0）、B（0，4），

∴OA＝4，OB＝4，

∴S△AOB＝×4×4＝8，

当直线l把△AOB的面积分为S△AOC：S△BOC＝2：3时，S△AOC＝，

作CF⊥OA于F，CE⊥OB于E，

∴×AOCF＝，即×4×CF＝，

∴CF＝．

当y＝时，x＝﹣，

则＝﹣k，

解得，k＝﹣，

∴直线l的解析式为y＝﹣x；

当直线l把△ABO的面积分为S△AOC：S△BOC＝3：2时，同理求得CF＝，

解得直线l的解析式为y＝﹣x．

故答案为y＝﹣x或y＝﹣x．