äãá¢áÖàï
Àƒäãá¢À¢1883áõȘçô¿ºò»îϥءþ¯ôÑ«¡þÀÊ¢çëÅÑ«Ø»àŠö£ÆÖØ£ä¾üÔÑöèüçáØ£ÅˋçÐçá¥₤¤üȘù■çáæ—ñ´àÓüôȤ
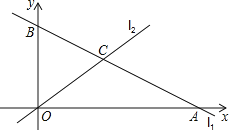
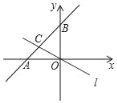
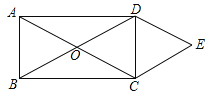
àÀأ侰ÊÑàöˆ1çáüÔÑöȘ§¨ù■à»çàñøȘàËç¶øÅ¥ðØ£ÑöȘÆÁüôê§ä¾üÔÑöȘÇÿç§çÖ1§æÑöÈ£§¨òÈüôçáê§ä¾üÔÑöåìñøÝÞà»çàñøȘ¡¼àËç¶øÅ¥ðØ£ÑöȘÆÁüôùáä¾üÔÑöȘÇÿç§çÖ2§æÑöÈ£å짨òÈùáä¾üÔÑöȘñøÝÞà»çàñøȘñøÝÞàËç¶øÅ¥ðØ£ÑöȘÆÁüô¯ùä¾üÔÑöȘÇÿç§çÖ3§æÑöȤÀÙÈ£íãîªçáýìæ¼Ø£øÝ¥äŽüôàËȘåÖý£Ñüñø¡ŸèÃ󺿻°äøÅȘùªÅö°èçáüÔÑöò»á¢å§âÇå§ÑÁȘ¯îíãøøñøÅöȘ°óæ¼¢çëÅÑ«çÐ¥₤ȘàÓë¥òú¢çëÅÑ«çÐ¥₤çá柰¾¥¡¡—§æÑöȘçÝÇÿç§çÖ5¡—§æÑöòÝȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ________È£çÝÇÿç§çÖ![]() ¡—§æÑöòÝÈ´
¡—§æÑöòÝÈ´![]() öˆí»í«ò»ÈˋȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ________.
öˆí»í«ò»ÈˋȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ________.

ÀƒÇÞ¯¡À¢![]()
![]()
Àƒ§ãö—À¢
¡ªƒïäãØãçûç§çÖöÍ¡—§æÑöòÝȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ![]() Șå·Æè¿Ìôè¢èçûçÝÇÿç§çÖ
Șå·Æè¿Ìôè¢èçûçÝÇÿç§çÖ![]() ¡—§æÑöòÝÈ´
¡—§æÑöòÝÈ´![]() öˆí»í«ò»ÈˋȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ
öˆí»í«ò»ÈˋȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ![]() .
.
¡ªƒïäãØãøˆÈ¤çÖØ£§æÑöòÝȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ![]() Ș
Ș
çÖѱ§æÑöòÝȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ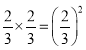 Ș
Ș
çÖ໧æÑöòÝȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ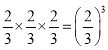 Ș
Ș
ÀÙ
ØåÇùâÁëóȘ
çÖöÍ¡—§æÑöòÝȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ![]() Ș
Ș
çÝÇÿç§çÖ![]() ¡—§æÑöòÝÈ´
¡—§æÑöòÝÈ´![]() öˆí»í«ò»ÈˋȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ
öˆí»í«ò»ÈˋȘÆÁüôçáüÔÑöçá°ÊÑàøÛ¤ëöˆ![]() .
.
¿òÇÞ¯¡È¤![]() È£
È£![]() .
.

 åáÑꢚ°çüçêÅÇÞ¯¡
åáÑꢚ°çüçêÅÇÞ¯¡