Question

如图（1），用形状相同、大小不等的三块直角三角形木板，恰好能拼成如图（2）所示的四边形ABCD、若AE=4，CE=3BE，那么这个四边形的面积是　_________　．

Answer 1

16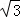

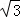
试题分析：∵形状相同、大小不等的三块直角三角形木板，
∴△ABE∽△ECD∽△DEA，∠B=∠C=∠AED=90°，
∴BE：CD=AB：EC，
∴四边形ABCD为矩形
∴AB=CD，
∴AB²=BE•EC，
∵CE=3BE，
∴AB=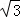BE，
∵AE=4，
∴BE=2，AB=2，
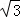∴BC=BE+CE=4BE=8，
∴这个四边形的面积是S=AB×BC=2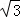×8=16．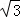
故填：16．
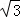点评：此题考查了直角三角形的性质和相似三角形的性质，同时也考查了勾股定理，解题时要注意认识图形