��Ŀ����
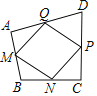
����Ŀ����ͼ���ڳ�����ABCD�У�AB��4cm��BE��5cm����E��AD���ϵ�һ�㣬AE��DE�ֱ�acm��bcm������(a��3)2��|2a��b��9|��0������P��B���������2cm/s���ٶ���B��C��D�˶������յ����D�����˶�ʱ��Ϊt s��
��1��a��______cm��b��______cm��
��2��tΪ��ֵʱ��EP���ı���BCDE���ܳ�ƽ�֣�
��3������һ��Q�ӵ�E����������E��D��C��·���˶������ٶ�Ϊ1cm/s����P��Q����ͬʱ������������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶�����tΪ��ֵʱ����BPQ���������6cm2��


���𰸡���1��3��3����2��t��2s����3��t��![]() s��
s��![]() s��5s��
s��5s��
��������
��1�����ݷǸ��������ʼ������a��b��ֵ��
��2��������ı���BCDE���ܳ�������ED+DC=7��9�жϳ���P��BC�ϣ��Ӷ��õ�BP��ֵ���������ݵ�P���ٶ����ʱ�伴�ɣ�
��3���ֱ�Ե�P�͵�Q��λ�ý��з������ۣ�����0��t��3������3��t��![]() ������
������![]() ��t��5���������BPQ��������г����̼��ɽ��
��t��5���������BPQ��������г����̼��ɽ��
�⣺��1����(a��3)2��|2a��b��9|��0��
��a��3=0��2a��b��9��
��ã�a=3��b=3��
�ʴ�Ϊ��3��3��
��2��C�ı���BCDE��BC��CD��DE��EB��18cm
��EP���ı���BCDE���ܳ�ƽ�֣�
��ED+DC=7��9��
���P��BC�ϣ�
��BE+BP=9cm��
BP��4cm��
��t��![]() ��2s��
��2s��
�൱tΪ2sʱ��EP���ı���BCDE���ܳ�ƽ�֣�
��3����BC=6��ED=3��DC=4��
�൱��P���Q����ʱ��2t+t=6+3+4����ã�t=![]() s��
s��
��t=3ʱ����P�����C����Q�����D��
��t=5ʱ����P�����D�������˶�ֹͣ��
����0��t��3����P��BC�ϣ���ʱ��Q���߶�ED�ϣ���ͼ1��
��![]() ��
��
��ã�t��![]() s��
s��
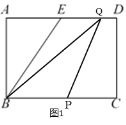
����3��t��![]() ������ǰ����ʱ��P����Q����CD�ϣ���ͼ2��
������ǰ����ʱ��P����Q����CD�ϣ���ͼ2��
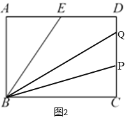
��PC=2t-6��CQ=3+4-t��
��PQ=3+4-t-(2t-6)
![]()
��ã�t��![]() s��
s��
����![]() ��t��5��������P����Q����CD�ϣ���ͼ3��
��t��5��������P����Q����CD�ϣ���ͼ3��
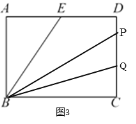
��PQ=PC-CQ=2t-6-(7-t)=3t-13��
��![]()
��ã�t��5s
�����ϣ�t��![]() s��
s��![]() s��5s��
s��5s��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�