题目内容
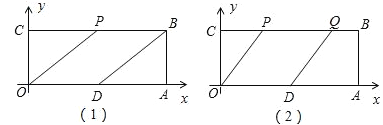
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.

(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值;若不存在,请说明理由;
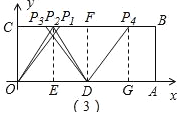
(3)△OPD为等腰三角形时,写出点P的坐标(不必写过程).
【答案】(1)5;(2)3;(3)P1(3,4),P2(2.5,4),P3(2,4),P4(8,4).
【解析】
试题分析:(1)根据平行四边形的性质就可以知道PB=5,可以求出PC=5,从而可以求出t的值.
(2)要使ODQP为菱形,可以得出PO=5,由三角形的勾股定理就可以求出CP的值而求出t的值.
(3)当P1O=OD=5或P2O=P2D或P3D=OD=5或P4D=OD=5时分别作P2E⊥OA于E,DF⊥BC于F,P4G⊥OA于G,利用勾股定理求得P1C,OE,P3F,DG的值,就可以求出P的坐标.
试题解析:(1)∵四边形PODB是平行四边形,
∴PB=OD=5,
∴PC=5,
∴t=5;
(2)∵四边形ODQP为菱形,
∴OD=OP=PQ=5,
∴在Rt△OPC中,由勾股定理得:
PC=3
∴t=3;
(3)当P1O=OD=5时,由勾股定理可以求得P1C=3,
P2O=P2D时,作P2E⊥OA,
∴OE=ED=2.5;
当P3D=OD=5时,作DF⊥BC,由勾股定理,得P3F=3,
∴P3C=2;
当P4D=OD=5时,作P4G⊥OA,由勾股定理,得
DG=3,
∴OG=8.
∴P1(3,4),P2(2.5,4),P3(2,4),P4(8,4).

练习册系列答案
相关题目