题目内容
【题目】知识储备
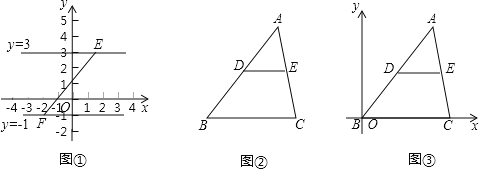
如图①，点E、F分别是y＝3和y＝﹣1上的动点，则EF的最小值是 ；
方法储备
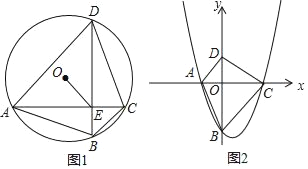
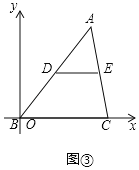
直角坐标系的建立，在代数和几何之间架起了一座桥梁，用代数的方法解决几何问题：某数学小组在自主学习时了解了三角形的中位线及相关的定理，在学习了《坐标与位置）后，该小组同学深入思考，利用中点坐标公式，给出了三角形中位线定理的一种证明方法．如图②，在△ABC中，点D，E分别是AB，AC边的中点，DE称为△ABC的中位线，则DE∥BC且DE＝
BC．该数学小组建立如图③的直角坐标系，设点A（a，b），点C （0，c）（c＞0）．请你利用该数学学习小组的思路证明DE∥BC且DE＝BC．（提示：中点坐标公式，A（x1，y1），B（x2，y2），则A，B中点坐标为（
，
）．
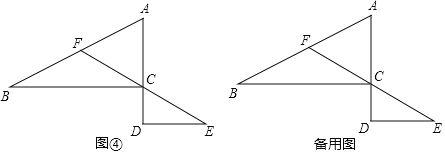
综合应用
结合上述知识和方法解决问题，如图④，在△ABC中，∠ACB＝90°，AC＝3，BC＝6，延长AC至点 D．DE⊥AD，连接EC并延长交AB边于点F．若2CD+DE＝6，则EF是否存在最小值，若存在，求出最小值；若不存在，请说明理由．
【答案】知识储备： 4；方法储备：见解析；综合应用：EF存在最小值，最小值为
．
【解析】
知识储备：根据垂线段最短，平行线之间的距离解决问题即可．
方法储备：如图③中，设
，
．利用中点坐标公式求解即可．
综合运用：建立如图平面直角坐标系，设
，则
．求出点
的运动轨迹，转化为知识储备的类型即可解决问题．
解：知识储备：如图①，点、
分别是
和
上的动点，则
的最小值是
，
故答案为4；
方法储备：如图③中，设，．
，
，
，
，
，，
，
，
，
；
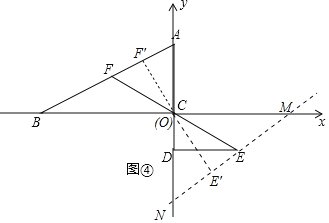
综合应用：建立如图平面直角坐标系，设，则．
，
，
点的运动轨迹是直线
，设这条直线与
轴交于
，由
轴交于
．
，
，
直线
的解析式为
，
，
根据垂线段最短可知，当
时，长最小，
作
于
，交
于
．
，
，
，
，
直线与直线关于原点
对称，
根据对称性可知
，
的最小值
．
