Question

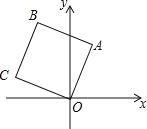
【题目】如图1，平行四边形在平面直角坐标系中，其中点的坐标分别是，，点在轴正半轴上，点为的中点，点在轴正半轴上，

（1）点的坐标为______，点的坐标为_______．

（2）求点的坐标．

（3）如图2，根据（2）中结论，将顺时针旋转至，求的长度．

Answer 1

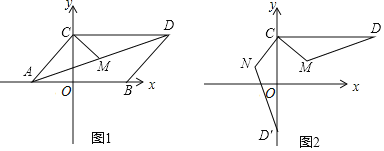
【答案】（1）（0，2）；（3，0）；（2）（，1）；（3）．

【解析】

（1）由平行四边形的性质可得AB=CD，AB∥CD，由点C在y轴正半轴上，D的坐标是（5，2），可得CD=AB=5，即可求点C，点B坐标；
（2）由中点坐标公式可求点M坐标；
（3）由两点距离公式可求CM的长，由旋转的性质可得△CMN是等腰直角三角形，由直角三角形的性质可求MN的长．

解：（1）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∵点C在y轴正半轴上，D的坐标是（5，2），
∴点C坐标为（0，2），CD=5，
∴AB=CD=5，

又点A（-2，0），
∴点B（3，0）
故答案为：（0，2）；（3，0）；
（2）∵点M为AD的中点，且点A，D的坐标分别是（-2，0），（5，2），
∴点M（，1）；
（3）∵点M（，1），点C（0，2），
∴CM=，

∵将△CMD顺时针旋转90°至△CND′，
∴CM=CN=，∠MCN=90°，
∴△CMN是等腰直角三角形，
∴MN=．