题目内容
【题目】如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均分成4个长方形,然后按图2形状拼成一个正方形.
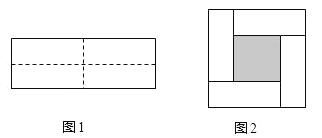
(1)图2中阴影部分的边长是 (用含a、b的式子表示);
(2)若2a+b=7,且ab=3,求图2中阴影部分的面积;
(3)观察图2,用等式表示出(2a﹣b)2,ab,(2a+b)2的数量关系是 .
【答案】(1)2a-b;(2)25;(3)(2a+b)2﹣(2a﹣b)2=8ab.
【解析】
(1)观察由已知图形,得到四个小长方形的长为2a,宽为b,那么图2中的空白部分的正方形的边长是小长方形的长减去小长方形的宽.
(2)通过观察图形,大正方形的边长为小长方形的长和宽的和.图2中空白部分的正方形的面积为大正方形的面积减去四个小长方形的面积.
(3)通过观察图形知:(2a+b)2,(2a-b)2, 8ab.分别表示的是大正方形、空白部分的正方形及小长方形的面积.
(1)图2的阴影部分的边长是2a﹣b.
故答案为:2a﹣b;
(2)由图2可知,阴影部分的面积=大正方形的面积﹣4个小长方形的面积.
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49.
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,∴阴影部分的面积=(2a﹣b)2=49﹣24=25;
(3)由图2可以看出,大正方形面积=阴影部分的正方形的面积+四个小长方形的面积,即:(2a+b)2﹣(2a﹣b)2=8ab.
故答案为:(2a+b)2﹣(2a﹣b)2=8ab.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】我市某校准备组织学生及学生家长坐高铁到杭州进行社会实践,为了便于管理.所有人员必须乘坐在同一列高铁上.根据报名人数,若都买一等座单程火车票需6560元,若都买二等座单程火车票,则需3120元(学生票二等座打7.5折,一等座不打折).已知学生家长与教师的人数之比为3:1,余姚北站到杭州东站的火车票价格如表所示:
运行区间 | 票价 | ||
上车站 | 下车站 | 一等座 | 二等座 |
余姚北 | 杭州东 | 82(元) | 48(元) |
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买m张(m小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y(元)(用含m的代数式表示).