题目内容
【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G. 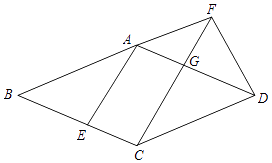
求证:
(1)FD=CG;
(2)CG2=FGFC.
【答案】
(1)证明:∵在菱形ABCD中,AD∥BC,
∴∠FAD=∠B,
在△ADF与△BAE中, 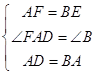 ,
,
∴△ADF≌△BAE,
∴FD=EA,
∵CF∥AE,AG∥CE,
∴EA=CG,
∴FD=CG
(2)解:∵在菱形ABCD中,CD∥AB,
∴∠DCF=∠BFC,
∵CF∥AE,
∴∠BAE=∠BFC,
∴∠DCF=∠BAE,
∵△ADF≌△BAE,
∴∠BAE=∠FDA,
∴∠DCF=∠FDA,
又∵∠DFG=∠CFD,
∴△FDG∽△FCD,
∴ ![]() ,FD2=FGFC,
,FD2=FGFC,
∵FD=CG,
∴CG2=FGFC
【解析】(1)根据菱形的性质得到∠FAD=∠B,根据全等三角形的性质得到FD=EA,于是得到结论;(2)根据菱形的性质得到∠DCF=∠BFC,根据平行线的性质得到∠BAE=∠BFC,根据全等三角形的性质得到∠BAE=∠FDA,等量代换得到∠DCF=∠FDA,根据相似三角形的判定和性质即可得到结论.
【考点精析】通过灵活运用菱形的性质和相似三角形的判定与性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
相关题目