题目内容
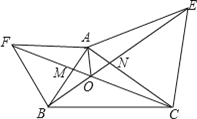
【题目】如图,直线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上,连接
的图象上,连接![]() .
.
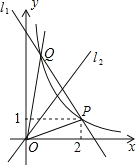
(1)求直线![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)直线![]() 经过点
经过点![]() 吗?请说明理由;
吗?请说明理由;
(3)当直线![]() 与反比例数
与反比例数![]() 图象的交点在
图象的交点在![]() 两点之间.且将
两点之间.且将![]() 分成的两个三角形面积之比为
分成的两个三角形面积之比为![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 经过点
经过点![]() ,理由见解析;(3)
,理由见解析;(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)依据直线l1:y=-2x+b和反比例数![]() 的图象都经过点P(2,1),可得b=5,m=2,进而得出直线l1和反比例函数的表达式;
的图象都经过点P(2,1),可得b=5,m=2,进而得出直线l1和反比例函数的表达式;
(2)先根据反比例函数解析式求得点Q的坐标为![]() ,依据当
,依据当![]() 时,y=-2×
时,y=-2×![]() +5=4,可得直线l1经过点Q;
+5=4,可得直线l1经过点Q;
(3)根据OM将![]() 分成的两个三角形面积之比为
分成的两个三角形面积之比为![]() ,分以下两种情况:①△OMQ的面积:△OMP的面积=1:2,此时有QM:PM=1:2;②OMQ的面积:△OMP的面积=2:1,此时有QM:PM=2:1,再过M,Q分别作x轴,y轴的垂线,设点M的坐标为(a,b),根据平行线分线段成比例列方程求解得出点M的坐标,从而求出k的值.
,分以下两种情况:①△OMQ的面积:△OMP的面积=1:2,此时有QM:PM=1:2;②OMQ的面积:△OMP的面积=2:1,此时有QM:PM=2:1,再过M,Q分别作x轴,y轴的垂线,设点M的坐标为(a,b),根据平行线分线段成比例列方程求解得出点M的坐标,从而求出k的值.
解:(1)∵![]() 直线和反比例函数
直线和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,
,
![]() .
.
![]()
∴直线l1的解析式为y=-2x+5,反比例函数大家解析式为![]() ;
;
(2)直线![]() 经过点
经过点![]() ,理由如下.
,理由如下.![]() 点
点![]() 在反比例函数的图象上,
在反比例函数的图象上,
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 当
当![]() 时,
时,![]() .
.
![]() 直线
直线![]() 经过点
经过点![]() ;
;
(3)![]() 的值为
的值为![]() 或
或![]() .理由如下:
.理由如下:
OM将![]() 分成的两个三角形面积之比为
分成的两个三角形面积之比为![]() ,分以下两种情况:
,分以下两种情况:
①△OMQ的面积:△OMP的面积=1:2,此时有QM:PM=1:2,
如图,过点M作ME⊥x轴交PC于点E,MF⊥y轴于点F;过点Q作QA⊥x轴交PC于点A,作QB⊥y轴于点B,交FM于点G,设点M的坐标为(a,b),
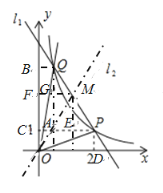
图①
∵点P的坐标为(2,1),点Q的坐标为(![]() ,4),
,4),
∴AE=a-![]() ,PE=2-a,
,PE=2-a,
∵ME∥BC,QM:PM=1:2,
∴AE:PE=1:2,
∴2-a=2(a-![]() ),解得a=1,
),解得a=1,
同理根据FM∥AP,根据QG:AG=QM:PM=1:2,
可得(4-b):(b-1)=1:2,解得b=3.
所以点M的坐标为(1,3),代入y=kx可得k=3;
②OMQ的面积:△OMP的面积=2:1,此时有QM:PM=2:1,如图②,

图②
同理可得点M的坐标为(![]() ,2),代入y=kx可得k=
,2),代入y=kx可得k=![]() .
.
故k的值为3或![]() .
.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案