Question

【题目】如图1，在平面直角坐标系中，已知抛物线与轴交于，两点，与轴交于点．

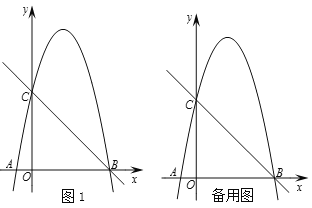
（1）求抛物线的函数表达式；

（2）若点P是位于直线BC上方抛物线上的一个动点，求△BPC面积的最大值；

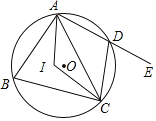
（3）若点D是y轴上的一点，且以B,C,D为顶点的三角形与相似，求点D的坐标；

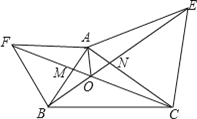
（4）若点E为抛物线的顶点，点F（3，a)是该抛物线上的一点，在轴、轴上分别找点M、N，使四边形EFMN的周长最小，求出点M、N的坐标．

Answer 1

【答案】（1）；（2）△BPC面积的最大值为 ；（3）D的坐标为（0，1）或（0，）；（4）M（，0），N（0，）

【解析】

（1）抛物线的表达式为：y=a（x+1）（x-5）=a（x2-4x-5），即-5a=5，解得：a=-1，即可求解；

（2）利用S△BPC=×PH×OB=（-x2+4x+5+x-5）=（x-）2+，即可求解；

（3）B、C、D为顶点的三角形与△ABC相似有两种情况，分别求解即可；

（4）作点E关于y轴的对称点E′（-2，9），作点F（2，9）关于x轴的对称点F′（3，-8），连接E′、F′分别交x、y轴于点M、N，此时，四边形EFMN的周长最小，即可求解．

解：（1）把，分别代入得：

∴

∴抛物线的表达式为：．

（2）如图，过点P作PH⊥OB交BC于点H

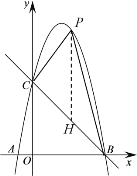
令x=0，得y=5

∴C（0，5），而B（5，0）

∴设直线BC的表达式为：

∴

∴

设，则

∴

∴

∴

∴△BPC面积的最大值为．

（3）如图，∵ C（0，5），B（5，0）

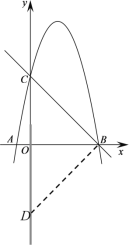
∴OC=OB，

∴∠OBC=∠OCB=45°

∴AB=6，BC=

要使△BCD与△ABC相似

则有或

①当时

∴

则

∴D（0，）

② 当时，

CD=AB=6，

∴D（0，1）

即：D的坐标为（0，1）或（0，）

（4）∵

∵E为抛物线的顶点，

∴E（2，9）

如图，作点E关于y轴的对称点E'（﹣2，9），

∵span>F（3，a）在抛物线上，

∴F（3，8），

∴作点F关于x轴的对称点F'（3，8），

则直线E' F'与x轴、y轴的交点即为点M、N

设直线E' F'的解析式为：

则

∴

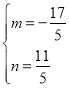
∴直线E' F'的解析式为：

∴，0），N（0，）．