题目内容
【题目】如图,△ABC和△ADE是两个不全等的等腰直角三角形,其中点B与点D是直角顶点,现固定△ABC,而将△ADE绕点A在平面内旋转.
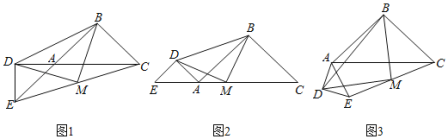
(1)如图1,当点D在CA延长线上时,点M为EC的中点,求证:△DMB是等腰三角形.
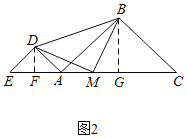
(2)如图2,当点E在CA延长线上时,M是EC上一点,若△DMB是等腰直角三角形,∠DMB为直角,求证:点M是EC的中点.
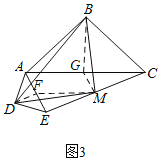
(3)如图3,当△ADE绕点A旋转任意角度时,线段EC上是否都存在点M,使△BMD为等腰直角三角形,若不存在,请举出反例;若存在,请予以证明.
【答案】(1)见解析;(2)见解析;(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,理由见解析
【解析】
(1)利用直角三角形斜边上的中线等于斜边的一半得出BM=DM=![]() EC,即可得出答案;
EC,即可得出答案;
(2)根据AAS证明△DFM≌∠MGB,得FM=BG,DF=MG,根据线段的和表示EM和MC,可得结论;
(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,作辅助线,构建全等三角形,证明△DFM≌∠MGB(SAS),得BM=DM,∠FMD=∠GBM,再证明∠DMB=90°,可得结论.
(1)如图1,∵∠EDC=90°,点M为EC的中点,
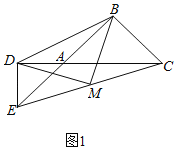
∴DM=![]() EC.
EC.
同理可得:BM=![]() EC.
EC.
∴DM=BM,
∴△DMB是等腰三角形;
(2)过点D作DF⊥EA,过点B作BG⊥AC,
∵△ABC和△ADE是两个等腰直角三角形,
∴BG=GC=AG,DF=EF=FA,
∴∠DFM=∠BGM=90°,
∴∠FDM+∠DMF=90°,
∵△DMB是等腰直角三角形,
∴DM=BM,∠DMB=90°,
∴∠BMG+∠DMF=90°,
∴∠FDM=∠BMG,
∴△DFM≌∠MGB(AAS),
∴FM=BG,DF=MG,
∵BG=GC,DF=EF,
∴FM=GC,MG=EF,
∵EM=EF+FM,MC=MG+GC,
∴EM=MC,
∴点M是EC的中点;
(3)线段EC上都存在中点M,使△BMD为等腰直角三角形,
理由是:取AE中点F,AC中点G,连接FD,FM,BG,GM,
∵点M是EC的中点,点G是AC的中点,
∴GM=![]() AE,GM∥AE,BG⊥AC,∠BGC=90
AE,GM∥AE,BG⊥AC,∠BGC=90![]() ,
,
∵F是AE中点,
∴AF=![]() AE,DF⊥AE,∠DFE=90
AE,DF⊥AE,∠DFE=90![]() ,
,
∴AF∥GM,AF=GM,
∴四边形AFMG是平行四边形,
∴∠AFM=∠AGM,
∴∠EFM=∠MGC.
∵∠DFM=∠EFM+∠DFE=∠EFM+90![]() ,
,
∠BGM=∠MGC+∠BGC=∠MGC+90![]() ,
,
∴∠DFM=∠BGM,
∵GM=AF=DF,
∴DF=GM,
同理可得 BG=FM,
∴△DFM≌∠MGB(SAS),
∴BM=DM,∠FMD=∠GBM,
∵FM∥AC,
∴∠FMG=∠CGM,
∴∠DMB=∠FMD+∠FMG+∠GMB,
=∠GBM+∠CGM+∠GMB,
=180°﹣∠BGC,
=90°,
∴△BMD是等腰直角三角形.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】某商场用两个月时间试销某种新型商品,经市场调查,该商品的第![]() 天的进价
天的进价![]() (元/件)与
(元/件)与![]() (天)之间的相关信息如下表:
(天)之间的相关信息如下表:
时间 |
|
|
进价 |
| 40 |
该商品在销售过程中,销售量![]() (件)与
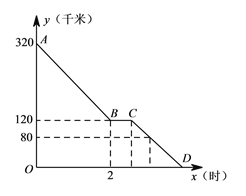
(件)与![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
在销售过程中,商场每天销售的该产品以每件80元的价格全部售出.
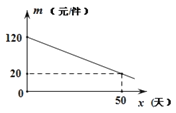
(1)求该商品的销售量![]() (件)与
(件)与![]() (天)之间的函数关系;
(天)之间的函数关系;
(2)设第![]() 天该商场销售该商品获得的利润为
天该商场销售该商品获得的利润为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
(3)在销售过程中,当天的销售利润不低于2400元的共有多少天?