题目内容
如图,正方形 的边长为2,以
的边长为2,以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;然后以
;然后以 为对角线作正方形
为对角线作正方形 ,又以
,又以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 .则:(1)
.则:(1) = ;(2)
= ;(2) = .
= .

 的边长为2,以
的边长为2,以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;然后以
;然后以 为对角线作正方形
为对角线作正方形 ,又以
,又以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 .则:(1)
.则:(1) = ;(2)
= ;(2) = .
= .
(1) 4-π.(2)  .
.
 .
.试题分析:第一个阴影部分的面积都等于它所在正方形的面积-扇形的面积.依此公式计算.
S1=4-
 =4-π.
=4-π.根据勾股定理得:OB1=

则OB2=2,
∴B1B2=
 -2,
-2,再根据勾股定理得:2OA22=(
 -2)2解得:OA22=6-
-2)2解得:OA22=6- .
.则阴影的面积=6-
 -
- =6-
=6- -
- .
.从而我们可以发现规律,并用Sn=
 表示.
表示.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
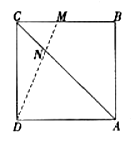

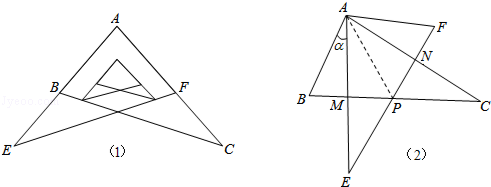
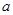 ,AM=
,AM=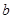 ,则CD的长为( )
,则CD的长为( )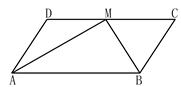
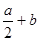

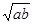
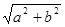

 ”,那么四边形ABCD一定是平行四边形;
”,那么四边形ABCD一定是平行四边形; ”,那么四边形ABCD一定是平行四边形
”,那么四边形ABCD一定是平行四边形