题目内容
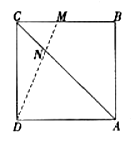
如图,在边长为6的正方形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N,若点M运动所经过的路程为x(6≤x≤12),那么当△ADN为等腰三角形时,x的值为___________。

6、12、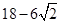 (少一个扣1分)
(少一个扣1分)
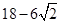 (少一个扣1分)
(少一个扣1分)试题分析:根据正方形的性质点M与点B、C重合时△ADN是等腰三角形;AN=AD时,利用勾股定理列式求出AC,再求出CN,然后求出△ADN和△CMN相似,利用相似三角形对应边成比例列式求出CM,然后求出BM即可得解.
试题解析:∵四边形ABCD是正方形,
∴当x=6时,点M与点B重合,AN=DN,△ADN为等腰三角形,
当x=12时,点M与点C重合,AD=DN,△ADN为等腰三角形,
当AN=AD时,在Rt△ACD中,AC=6
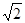 CN=AC-AN=6
CN=AC-AN=6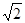 -6
-6∵正方形ABCD的边BC∥AD,
∴△ADN∽△CMN,
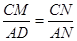 ,即
,即 ,解得CM=6
,解得CM=6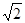 -6,
-6,∴BM=BC-AM=6-(6
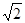 -6)=12-6
-6)=12-6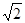 x=AB+BM=6+12-6
x=AB+BM=6+12-6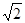 =18-6
=18-6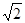
综上所述,x为6或12或18-6
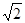 时,△ADN为等腰三角形.
时,△ADN为等腰三角形.故答案为:6或12或18-6
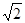 .
.
练习册系列答案
相关题目

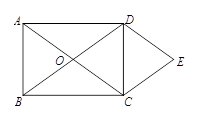
 中,
中, ,
, 为平面内一动点,
为平面内一动点, ,
, ,其中a,b为常数,且
,其中a,b为常数,且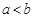 .将
.将 沿射线
沿射线 方向平移,得到
方向平移,得到 ,点A、B、D的对应点分别为点F、C、E.连接
,点A、B、D的对应点分别为点F、C、E.连接 .
. ,求
,求 的式子表示);
的式子表示); ,当线段
,当线段 的大小为__________;当线段
的大小为__________;当线段 的式子表示).
的式子表示).

 ,一边长是4cm,那么对角线长是___ ____;已知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm
,一边长是4cm,那么对角线长是___ ____;已知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm
 的边长为2,以
的边长为2,以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;然后以
;然后以 为对角线作正方形
为对角线作正方形 ,又以
,又以 为半径作弧
为半径作弧 交
交 ,设弧
,设弧 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 .则:(1)
.则:(1)
 ),则D点的坐标是 。
),则D点的坐标是 。