题目内容
如图,已知二次函数y=x2-3x-4的图象交x轴于A、B两点.
(1)若点P在线段AB上运动,作PQ⊥x轴,交抛物线于点Q,求PQ的最大值;
(2)已知点D(5,6)在抛物线上,若点M在线段AD上运动,作MN⊥x轴,交抛物线于点N,求MN的最大值;
(3)在(2)的运动过程中,求△ADN面积的最大值.

(1)若点P在线段AB上运动,作PQ⊥x轴,交抛物线于点Q,求PQ的最大值;
(2)已知点D(5,6)在抛物线上,若点M在线段AD上运动,作MN⊥x轴,交抛物线于点N,求MN的最大值;
(3)在(2)的运动过程中,求△ADN面积的最大值.

(1)当Q为抛物线的顶点时,PQ取得最大值.
∵y=x2-3x-4=(x-
)2-
,
∴点Q坐标为(
,-
),
∴PQ的最大值为
;
(2)∵D(5,6),A(-1,0),
设直线AD的解析式为:y=kx+b,则
,
解得
.
∴直线AD的解析式为:y=x+1;
设M(x,x+1),则N(x,x2-3x-4),
∴MN=x+1-(x2-3x-4)=-x2+4x+5=-(x-2)2+9,
∴当x=2时,MN的最大值为9;
(3)S△ADN=S△ANM+S△MDN=
MN•(5+1)=3MN,
∴由(2)的结论可得,当x=2时,△ADN面积的最大值为27.
∵y=x2-3x-4=(x-
| 3 |
| 2 |
| 25 |
| 4 |
∴点Q坐标为(
| 3 |
| 2 |
| 25 |
| 4 |
∴PQ的最大值为
| 25 |
| 4 |
(2)∵D(5,6),A(-1,0),
设直线AD的解析式为:y=kx+b,则
|
解得
|
∴直线AD的解析式为:y=x+1;
设M(x,x+1),则N(x,x2-3x-4),
∴MN=x+1-(x2-3x-4)=-x2+4x+5=-(x-2)2+9,
∴当x=2时,MN的最大值为9;
(3)S△ADN=S△ANM+S△MDN=
| 1 |
| 2 |
∴由(2)的结论可得,当x=2时,△ADN面积的最大值为27.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目

 点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______.
点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为______.

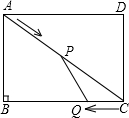 秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2.
秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2.