Question

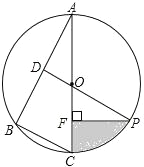
【题目】如图，在圆O中，弦AB＝8，点C在圆O上(C与A，B不重合)，连接CA、CB，过点O分别作OD⊥AC，OE⊥BC，垂足分别是点D、E．

(1)求线段DE的长；

(2)点O到AB的距离为3，求圆O的半径．

Answer 1

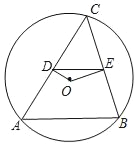
【答案】（1）DE＝4；（2）圆O的半径为5．

【解析】

(1)根据垂径定理得出AD=DC，CE=EB，再根据三角形的中位线定理可得DE=AB，代入相应数值求出即可；

(2)过点O作OH⊥AB，垂足为点H，则OH=3，连接OA，根据垂径定理可得AH=4，在Rt△AHO中，利用勾股定理求出AO的长即可得答案.

(1)∵OD经过圆心O，OD⊥AC，

∴AD=DC，

同理：CE=EB，

∴DE是△ABC的中位线，

∴DE=AB，

∵AB=8，

∴DE=4；

(2)过点O作OH⊥AB，垂足为点H，则OH=3，连接OA，

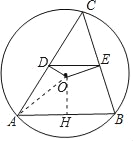
∵OH经过圆心O，

∴AH=BH=AB，

∵AB=8，

∴AH=4，

在Rt△AHO中，AH2+OH2=AO2，

∴AO=5，即圆O的半径为5．