Question

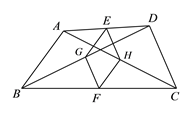
【题目】如图，在锐角△ABC中，AD是BC边上的高．∠BAF=∠CAG=90°，且AB=AF=AC=AG．连接FG，交DA的延长线于点E，连接BG，CF．下列结论：①∠FAG+∠BAC=180°；②BG=CF；③BG⊥CF；④∠EAF=∠ABC．其中一定正确的个数是（　　）

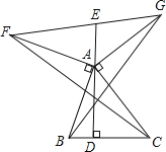
A.4个B.3个C.2个D.1个

Answer 1

【答案】A

【解析】

利用周角及∠BAF=∠CAG=90°，可推得①正确；易证得△CAF≌△GAB（SAS），从而推得②正确；利用△CAF≌△GAB及三角形内角和与对顶角，可判断③正确；利用等腰三角形三线合一性质及互余关系可推得④正确．

解：∵∠BAF=∠CAG=90°，

∴∠FAG+∠BAC=360°-90°-90°=180°，故①正确；

∵∠BAF=∠CAG=90°

∴∠BAF+∠BAC=∠CAG+∠BAC，即∠CAF=∠GAB

又∵AB=AF=AC=AG，

∴△CAF≌△GAB（SAS），

∴BG=CF，故②正确；

∵△FAC≌△BAG

∴∠FCA=∠BGA

又∵BC与AG所交的对顶角相等

∴BG与FC所交角等于∠GAC，即等于90°

∴BG⊥CF，故③正确；

∵AB=AC，AD⊥BC

∴∠BAD=∠CAD

∴∠EAF=∠CAG

∵∠EAF+∠BAD=∠ABC+∠BAD=90°

∴∠EAF=∠ABC，故④正确．

故选：A．