题目内容
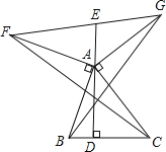
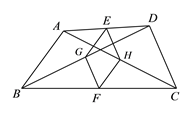
【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点.
(1)求证:四边形EGFH是菱形;
(2)若AB=4,且BA、CD延长后相交所成的锐角是60°,求四边形EGFH的面积.
【答案】(1)见解析;(2)![]()
【解析】(1)利用三角形中位线定理即可证明;
(2)由BA、CD延长后相交所成的锐角是60°,菱形EGFH有一个内角为60°,将菱形沿较短的对角线分割成两个全等的等边三角形,即可求出面积.
(1)∵E是AD的中点,G是BD的中点,
∴EG∥AB,EG=![]() AB,
AB,
同理FH∥AB,FH=![]() AB,EH∥CD,EH=
AB,EH∥CD,EH=![]() CD,FG∥CD,FG=
CD,FG∥CD,FG=![]() CD
CD
又AB=CD,
∴EG=GF=HF=EH,
∴四边形EGFH是菱形
(2)BA、CD延长后相交所成的角是60°,由上知∠EGH=60°,
即四边形EGFH是有一角为60°的菱形,
∵AB=4,
∴EG=2,
∴菱形EGFH的面积为![]() .
.

练习册系列答案
相关题目