题目内容
化简或化简求值
①3(x2-2xy)-[3x2-2y-2(3xy+y)]
②已知A=3a2+b2-5ab,B=2ab-3b2+4a2,先求-B+2A,并求当a=- ,b=2时,-B+2A的值.
,b=2时,-B+2A的值.
③如果代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x所取的值无关,试求代数式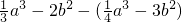 的值.
的值.
④有这样一道计算题:“计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中 ,y=-1”,甲同学把
,y=-1”,甲同学把 看错成
看错成 ;但计算结果仍正确,你说是怎么一回事?
;但计算结果仍正确,你说是怎么一回事?
解:①原式=3x2-6xy-[3x2-2y-6xy-2y],
=3x2-6xy-3x2+2y+6xy+2y,
=4y;
②-B+2A=-(2ab-3b2+4a2)+2(3a2+b2-5ab),
=2a2-12ab+5b2,
当a=- ,b=2时,
,b=2时,
原式=2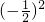 -12(-
-12(- )×(2)+5×22=32.5;
)×(2)+5×22=32.5;
③原式=(2x2+ax-y+6)-(2bx2-3x+5y-1),
=(2-2b)x2+(3+a)x-6y+7,
又因为所取值与x无关,可得a=-3,b=1,
又: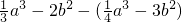 =
= a3+b2,
a3+b2,
当a=-3,b=1时,原式= a3+b2=-
a3+b2=-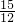 =-
=- ;
;
④原式=(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3),
=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3,
=-2y3,
因为结果中不含x所以与x取值无关.
分析:①先去括号,然后合并同类项得出最简整式.
②先将-B+2A所示的整式化为最简,然后代入a和b的值即可得出答案.
③与x的值无关则说明x项的系数为0,由此可得出a和b的值,将要求的代数式化为最简代入即可得出答案.
④将整式化简可得出最简整式不含x项,由此可得为什么计算结果仍正确.
点评:本题考查整式的化简求值,化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面,也是一个常考的题材.
=3x2-6xy-3x2+2y+6xy+2y,
=4y;
②-B+2A=-(2ab-3b2+4a2)+2(3a2+b2-5ab),
=2a2-12ab+5b2,
当a=-
 ,b=2时,
,b=2时,原式=2
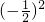 -12(-
-12(- )×(2)+5×22=32.5;
)×(2)+5×22=32.5;③原式=(2x2+ax-y+6)-(2bx2-3x+5y-1),
=(2-2b)x2+(3+a)x-6y+7,
又因为所取值与x无关,可得a=-3,b=1,
又:
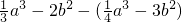 =
= a3+b2,
a3+b2,当a=-3,b=1时,原式=
 a3+b2=-
a3+b2=-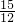 =-
=- ;
;④原式=(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3),
=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3,
=-2y3,
因为结果中不含x所以与x取值无关.
分析:①先去括号,然后合并同类项得出最简整式.
②先将-B+2A所示的整式化为最简,然后代入a和b的值即可得出答案.
③与x的值无关则说明x项的系数为0,由此可得出a和b的值,将要求的代数式化为最简代入即可得出答案.
④将整式化简可得出最简整式不含x项,由此可得为什么计算结果仍正确.
点评:本题考查整式的化简求值,化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面,也是一个常考的题材.

练习册系列答案
相关题目