��Ŀ����
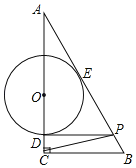
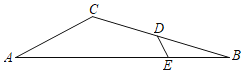
����Ŀ����֪��ABΪ��O��ֱ������BC��AF�ཻ�ڵ�E������E��ED��AB����AEC����BED��
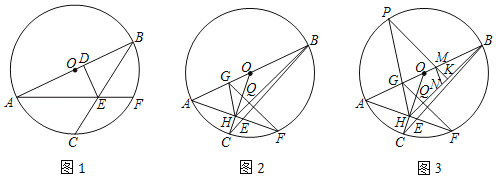
��1����ͼ1����֤��![]() ��
��
��2����ͼ2������BAF��45��ʱ��OC��AF�ڵ�H����FG��BH�ڵ�Q����AB�ڵ�G������GH����֤����AGH����BGF��
��3����ͼ3���ڣ�2���������£�����HG����O���ڵ�P������P��PK��BH��AB�ڵ�M������Ϊ��K����NΪBH���е㣬MN��![]() ������O�İ뾶��
������O�İ뾶��
���𰸡���1�������������2�������������3��6��
��������
��1����ͼ1������BF��֤��BDE�ա�BFE���Ƴ���ABC����FBC������Բ�ܽǶ��������ɵó����ۣ�
��2����ͼ2������OF��BF����AS��AF�ڵ�A����FG���ӳ����ڵ�S��֤��FSA�ա�BHF����֤��SAG�ա�HAG���ɵá�SGA����AGH�����ɵó����ۣ�
��3����ͼ3������O��OR��HP�ڵ�R��OT��BH�ڵ�T������BP�ֱ�֤��ORH�ա�OTH�͡�ORP�ա�OTB���Ƴ�PH��BH�����OPR����OBT�������Ƴ�PO��BO����OPB����OBP��45�㣬PG��PM��OG��OM������M��ML��BP�ڵ�L�����tan��PML��tan��PBH��2����BM��4a����BL��ML��2![]() a�����NΪBH���е㣬GH��2MN��
a�����NΪBH���е㣬GH��2MN��![]() ������G��GU��OH�ڵ�U����Rt��GUH�У������GU��
������G��GU��OH�ڵ�U����Rt��GUH�У������GU��![]() ���������a��ֵ���ɽ�һ�����OB�ij���
���������a��ֵ���ɽ�һ�����OB�ij���
��1����ͼ1������BF��
��ABΪ��O��ֱ����
���AFB��90�㣬
�ߡ�AEC����BED����AEC����BEF��
���BEF����BED��
��ED��AB��
���BDE����AFB��90�㣬
�֡�BE��BE��
���BDE�ա�BFE��AAS����
���ABC����FBC��
��![]() ��
��
��2����ͼ2������OF��BF����AS��AF�ڵ�A����FG���ӳ����ڵ�S��
��![]() ��
��
���AOC����FOC��
��AO��OF��
��OC��AF��
��AH��HF��![]() AF��
AF��
�ߡ�BAF��45�㣬��AFB=90��
��AF��BF��
��FG��BH��AS��AF��
���S����BHF��
�֡ߡ�SAF����HFB��90�㣬
���FSA�ա�BHF��AAS����
��AS��HF��AH��
�ߡ�SAG����GAH��45�㣬AG��AG��
���SAG�ա�HAG��SAS����
���SGA����AGH��
���AGH����BGF��
��3����ͼ3������O��OR��HP�ڵ�R��OT��BH�ڵ�T������BP��
�ߡ�SAG�ա�HAG��
���AHG����S����BHF��
��OH��AF��
���OHG����OHB��
�ߡ�ORH����OTH��90�㣬OH��OH��
���ORH�ա�OTH��AAS����
��RH��TH��OR��OT��
�֡�OP��OB����ORP����OTB��90�㣬
��Rt��ORP��Rt��OTB��HL����
��PR��BT��
��PR+RH��BT+TH��
��PH��BH��
���HPB����HBP��
���OPR����OBT������
�ߡ�AOH����A��45�㣬
���PHO����BHO����AOH����OBH��45�㩁����
���PHB��90�㩁2����
���HPB����HBP��45��+����
���PBO��45�㣬
��PO��BO��
���OPB����OBP��45�㣬
��PO��AB��
��PK��BH��GF��BH��
��PK��GF��
���PMG����BGF��
�ߡ�PGM����AGH����BGF��
���PGM����PMG��
��PG��PM��
��OG��OM��
����M��ML��BP�ڵ�L��
�ߡ�PBH����BHF��45��+����
��tan��PBH��tan��BHF��![]() ��2��
��2��
�ߡ�MPL����BPK��
���PML����PBH��
��tan��PML��tan��PBH��2��
��BM��4a����BL��ML��2![]() a��
a��
��PL��4![]() a��
a��
��PB��6![]() a��
a��
��PO��BO��6a��
��OM��OG��2a��
��GM��4a��
��GM��BM��
��NΪBH���е㣬
��MNΪBGH����λ�ߣ�
��GH��2MN��![]() ��
��
����G��GU��OH�ڵ�U��
��tan��GHO��tan��OHB��tan��FBH��![]() ��
��
��Rt��GUH����GU��b����UH��2b��GH��![]() b��
b��
��![]() b=
b=![]() ��
��
��GU��![]() ��
��
��GO��2��2a��
��a��1��
��OB��6a��6��
����O�İ뾶Ϊ6��




 Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�