题目内容
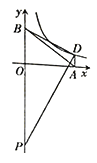
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,OA=4,AB=5,点D在反比例函数![]() (k>0)的图象上,
(k>0)的图象上,![]() ,点P在y轴负半轴上,OP=7.
,点P在y轴负半轴上,OP=7.
(1)求点B的坐标和线段PB的长;
(2)当![]() 时,求反比例函数的解析式。
时,求反比例函数的解析式。
【答案】(1)10(2)![]()
【解析】试题分析:(1)根据勾股定理求出OB,即可得出答案;(2)设D的坐标是(4,y),证△BDM∽△DPM,得出比例式,代入即可求出y,把D的坐标代入求出即可.
试题解析:(1)∵AB=5,OA=4,∠AOB=90°,
∴由勾股定理得:OB=3,即点B的坐标是(0,3).
∵OP=7,
∴线段PB=OB+OP=3+7=10.
(2)过点D作DM⊥y轴于M,

∵∠PDB=90°,
∴∠BDP=∠DMB=∠DMP=90°
∴∠DBM+∠BDM=90°,∠BDM+∠MDP=90°
∴∠DBM=∠MDP
∴△DBM∽△PDM
∴![]()
∵OA=4,DM⊥y轴,设D点的坐标为(4,y)(y>0),
∴![]() ,
,
解得y=1(y=-5舍去),
即点D的坐标为(4,1)
把点D的坐标代入![]() ,得k=4,即反比例函数的解析式是
,得k=4,即反比例函数的解析式是![]() .
.

练习册系列答案
相关题目
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?